Спектр дискретного сигнала

Преобразование Фурье позволяет вычислить спектральную плотность сигнала, представляющего собой функцию (как правило, времени либо пространственных координат). Дискретный же сигнал является последовательностью чисел, поэтому для анализа его спектра обычными (аналоговыми) средствами необходимо сопоставить этой последовательности некоторую функцию.

Традиционным способом такого сопоставления является представление отсчетов в виде дельта-функций с соответствующими множителями и задержками. Для последовательности отсчетов {x(k)} получится следующий сигнал:

(3.1)

Преобразование Фурье линейно, спектр дельта-функции равен единице, а задержка сигнала во времени приводит к умножению спектра на комплексную экспоненту. Все это (см. раздел «Свойства преобразования Фурье» главы 1) позволяет сразу же записать спектр дискретного сигнала:

(3.2)

Из этой формулы видно главное свойство спектра любого дискретного сигнала: спектр является периодическим, и его период в данном случае равен (то есть круговой частоте дискретизации, поскольку, составляя сигнал из дельта-функций, мы выбрали единичный интервал между ними, что дает ):

Следует также обратить внимание на размерность спектральной функции дис­кретного сигнала: она совпадает с размерностью отсчетов. Это связано с тем, что дельта-функции времени, из которых был составлен сигнал (3.1), имеют размерность частоты (см. раздел «Классификация сигналов» главы 1).

Формула (3.2) позволяет вычислить спектральную функцию по известным отсчетам x(k). При конечном числе ненулевых отсчетов этот расчет несложен; он может быть выполнен с помощью функции MATLAB freqz (подробнее об этой функции см. раздел «Расчет частотной характеристики» главы 4).

Теперь рассмотрим несколько иную задачу. Пусть значения x(k) являются отсчетами аналогового сигнала s(t), взятыми с периодом Г:

x(k) = s(kT).

Выясним, как в этом случае спектр дискретного сигнала (3.2) связан со спектром аналогового сигнала .

Итак, мы рассматриваем дискретизированный сигнал в виде последовательности дельта-функций, «взвешенной» значениями отсчетов s(kT) аналогового сигна­ла 5(0 (рис. 3.4):

(3.3)

Так как функция (t - kT) равна нулю всюду, кроме момента t = kT, можно заменить в выражении (3.3) константы s(kT) на исходный непрерывный сигнал s(t):

(3.4)

Далее заметим, что сумма, входящая в выражение (3.4), является периодическим сигналом, а потому может быть представлена в виде ряда Фурье. Коэффициенты этого ряда, согласно (1.9), равны

(3.5)

В формуле (3.5) было учтено, что в интервал интегрирования (-Т/2, Т/2) попадает только одна дельта-функция, соответствующая k = 0.

Таким образом, периодическая последовательность дельта-функций может быть представлена в виде комплексного ряда Фурье (1.8):

где . Подставив (3.6) в (3.4), получим

Умножение сигнала на ехр() соответствует сдвигу спектральной функции на , поэтому спектр дискретизированного сигнала можно записать следующим образом:

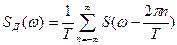
Таким образом, спектр дискретизированного сигнала представляет собой беско­нечный ряд сдвинутых копий спектра исходного непрерывного сигнала s(t) (рис. 3.5). Расстояние по частоте между соседними копиями спектра равно частоте дискретизации .

Следует также отметить, что из-за наличия в формуле (3.7) множителя 1 /Т спектр дискретизированного сигнала имеет размерность, совпадающую с размерностью сигнала (как уже говорилось, это связано с тем, что функция имеет размерность частоты).

Характер спектра дискретизированного сигнала еще раз демонстрирует частотно-временную дуальность преобразования Фурье:

В начале данного раздела мы получили формулу (3.2), позволяющую рассчитать спектр последовательности отсчетов {x(k)}, никак не связывая эти отсчеты с аналоговым сигналом. Только что полученная формула (3.7) предполагает, что отсчеты {x(k)} получены путем дискретизации аналогового сигнала s(t), и показывает связь между спектрами дискретизированного и аналогового сигналов. Следует подчеркнуть, что эти две формулы дают одинаковый результат.

Отсюда следует еще один важный факт. Соединить отсчеты {x(k)} для получения аналогового сигнала можно произвольным образом. В каждом случае аналоговый сигнал будет, разумеется, иметь свой спектр. Однако результат суммирования сдвинутых копий спектров по формуле (3.7) всегда будет одним и тем же, поскольку определяется только значениями дискретных отсчетов {x(k)} = {s(kT}} и формулой (3.2).

Рисунок 3.5 наглядно демонстрирует и способ восстановления непрерывного сигнала по дискретным отсчетам. Для этого необходимо пропустить дискретный сигнал через идеальный фильтр нижних частот (ФНЧ) с частотой среза, равной половине частоты дискретизации. АЧХ такого фильтра показана на рис. 3.5 пунктиром.

Очевидно, что точное восстановление сигнала возможно, если сдвинутые копии спектра не перекрываются. Из рис. 3.5 видно, что для этого необходимо, чтобы частота дискретизации как минимум в два раза превышала верхнюю граничную частоту в спектре сигнала:

(3.8)

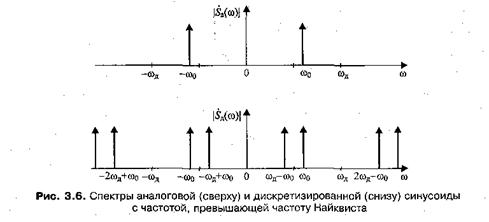
Спектральное представление дискретного сигнала позволяет объяснить появление ложных частот (aliasing). Пусть дискретизации подвергается гармонический сигнал с частотой , превышающей частоту Найквиста, но меньшей частоты дискретизации. Спектр такого сигнала показан на рис. 3.6 сверху. Сдвинутые копии спектра, возникающие при дискретизации, создают попадающие в полосу восстановления (от нуля до частоты Найквиста) спектральные составляющие с частотой (рис. 3.6, снизу). Спектры, получающиеся после дискретизации гармонических сигналов с частотами и , оказываются идентичными. Данный рисунок иллюстрирует в частотной области процесс дискретизации гармонического сигнала, показанный ранее на рис. 3.3.

В случае произвольного сигнала, если условие (3.8) не выполняется, сдвинутые копии спектра будут накладываться друг на друга, что приведет к неизбежным искажениям при восстановлении непрерывного сигнала (рис. 3.7).

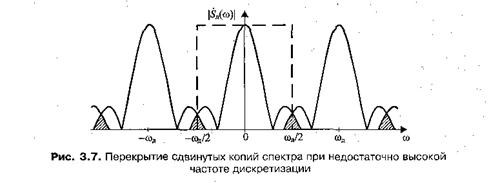
Эти искажения вызваны тем, что спектральные составляющие сигнала с частотами, превышающими частоту Найквиста, равную /2, не могут быть восстановлены правильно — вместо этого они вызывают наложение «хвостов» соседних сдвинутых копий спектра и появление ложных частот.

Если подлежащий дискретизации сигнал может содержать спектральные составляющие с частотами, превышающими частоту Найквиста, полезно предварительно пропустить его через ФНЧ с частотой среза, равной частоте Найквиста (рис. 3.8). При этом все равно будут потеряны высокочастотные составляющие — сохранить их можно лишь путем повышения частоты дискретизации. Однако в этом случае благодаря отсутствию наложения «хвостов» не произойдет появления ложных частот и диапазон частот 0... /2 будет представлен в дискретном сигнале без искажений.

Поиск по сайту: