Анализ изменения пространственного спектра фазовой решетки при смещении ее вдоль оси 0х

Функцию пропускания фазовой решетки запишем в виде

. (1.89)

Здесь -смещение функции вдоль оси 0х.

Примем к сведению, что ранее мы нашли спектр несмещенной фазовой решетки с функцией пропускания, заданной выражением (1.78).

Используем теорему о Фурье-образе смещенной функции, которая формулируется следующим образом:

если т.е. если ,

то Фурье-преобразование смещенной функции определяется формулой

(1.90)

Доказательство. Заменив , т.е. , получим

. (1.91)

Таким образом, при сдвиге функции 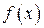на величину Фурье-образ этой функции умножается на .

Применив теорему смещения к нашей задаче, получим из соотношений (1.81) и (1.90) следующее выражение

. (1.92)

При переходе к анализу пространственного спектра решетки с конечными размерами следует заменить функции и на функции, которые являются Фурье образами апертурной функции, т.е. , .

1.8.5. Дифракция оптической волны на движущейся решетке

Положим, что дифракционная решетка движется в направлении 0х (т.е. поперек штрихов) с некоторой скоростью V. Подобная ситуация встречается на практике при анализе дифракции света на бегущей ультразвуковой (акустической) волне, которая распространяется в упругой среде. Ультразвуковая волна создает периодические возмущения показателя преломления упругой среды с периодом, равным длине волны 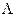, которые движутся со скоростью ультразвуковой волны. При прохождении световой волны через область, возмущенную ультразвуковой волной, перпендикулярно направлению ее движения, появляется пространственная фазовая модуляция волнового фронта световой волны с периодом, равным длине ультразвуковой волны.

В выражении (1.89) заменим , где V - скорость движения решетки, t - время. Тогда выражение (1.92) для пространственного спектра можно записать в виде

(1.93)

Здесь 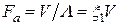- частота, с которой периодические возмущения (штрихи решетки) проходят через точку начала координат. По сравнению с дифракцией на неподвижной решетке здесь имеется отличие: появляется дополнительный множитель . Для того, чтобы наглядно продемонстрировать физический смысл этого множителя, дополним каждую из компонент пространственного спектра множителями, которые ранее были отброшены для сокращения записи, а именно:

.

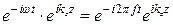Здесь f – частота световой волны. В результате множитель, характеризующий зависимость от времени в формуле (1.93) примет вид:

.

Это означает, что частота световой волны в дифракционном порядке с номером т отличается от частоты f световой волны, падающей на дифракционную решетку, на величину , т.е. на величину, кратную частоте акустической волны. Так, например, в первом порядке дифракции световая волна будет иметь частоту 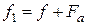, а в первом отрицательном порядке 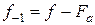. В результате наблюдается изменение (сдвиг) частоты дифрагированного света по отношению к частоте исходной световой волны. Это явление фактически является следствием эффекта Доплера, поскольку источниками дифрагированных волн являются частицы возмущенной среды, движущейся со скоростью акустической волны. Таким образом, во всех дифракционных порядках, кроме нулевого, имеет место сдвиг частоты света на величину, кратную частоте бегущей волны.

Условия, при которых данная модель дифракции на фазовой решетке применима для описания дифракции света на ультразвуковой волне, следующие:

· размер L акустического (звукового) столба в направлении движения световой волны ограничен условием, , где 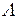- длина волны ультразвука, - длина волны света;

· свет падает по направлению, перпендикулярному к направлению распространения акустической волны, или под небольшим углом к нормали;

· взаимодействие происходит в изотропной среде.

Дифракция этого типа получила в литературе название «Дифракция Рамана – Ната». Более подробное описание можно найти, например, в книге [22]: М. Борн, Вольф "Основы оптики", глава 12, а также в специальной литературе по акустооптике.

1.8.6. Пространственный спектр дифрагированных волн при дифракции оптической волны на фазовой дифракционной решетке со ступенчатым профилем с формой меандра.

Рассмотрим фазовую дифракционную решетку со ступенчатым профилем, образованным выступами и впадинами одинаковой ширины на поверхности прозрачного материала (форма рельефа − меандр). Форма фазовой модуляции после взаимодействия оптической волны с такой решеткой изображена на рис.1.12., а функция модуляции волнового фронта описывается формулой (1.65): , где функция формы имеет вид (1.67):

Положим, что решетка однородна и бесконечна в направлении оси 0у, будем анализировать пространственный спектр дифрагированных волн в плоскости х0z. Реально решетка всегда имеет конечные размеры. Для упрощения расчетов можно воспользоваться моделью дифракционной решетки с бесконечным размером по координате х (подобно тому, как это было сделано ранее). Затем, используя полученный пространственный спектр в виде суммы d- функций и выполнив свертку этого спектра с функцией, описывающей спектр апертуры, можно получить пространственный спектр дифракции на решетке, ограниченной этой апертурой.

Следуя этому порядку, представим бесконечную периодическую функцию в виде разложения в ряд Фурье по гармоникам основной пространственной частоты .

. (1.94)

Коэффициенты Фурье выражаются формулами [21]*:

. (1.95)

. (1.96)

Проведем вычисление коэффициентов Фурье для заданной выше фазовой ступенчатой функции

. (1.97)

(1.98)

в частности:

(1.99)

Пусть на решетку падает слева плоская волна с амплитудой 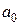. Пространственный спектр волны после прохождения дифракционной решетки имеет вид:

(1.100)

Здесь использовано представление в виде (1.94), а коэффициенты определяются выражениями (1.97), (1.98) (1.99).

Для физически реальной решетки с конечным размером апертуры решение получается из (1.100) путем свертки выражения (1.100) с выражением, описывающим пространственный спектр той апертуры, которая ограничивает размер дифракционной решетки. В результате получим пространственный спектр в виде:

, (1.101)

где коэффициенты определены выражениями (1.97), (1.98), (1.99). В случае, когда апертура имеет форму щели с размером D, функция имеет вид .

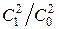Для того, чтобы сопоставить интенсивности дифрагированных пучков разных порядков, следует взять отношение квадратов коэффициентов . Например, отношение равно отношению интенсивностей первого порядка к нулевому. Для рассматриваемой фазовой решетки с профилем в виде меандра оно равно:

(1.102)

Следует заметить также, что при дифракции света на решетке типа меандра второй порядок дифракции отсутствует, поскольку .

Для третьего порядка получим:

(1.103)

Поиск по сайту: