 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Соотношение между мощностью падающего и дифрагированного излучения при дифракции света на амплитудной гармонической решетке
Взяв за основу проделанный выше расчет мощности для случая дифракции на щели, рассчитаем распределение мощности излучения по дифракционным порядкам при дифракции оптической волны с амплитудой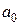 
на амплитудной дифракционной решетке с глубиной модуляции т. Построим диаграммы распределения мощности по порядкам дифракции, положив т = 1. Сравним полную падающую мощность и суммарную мощность излучения в дифракционных порядках. Проанализируем баланс мощности в системе и соотношение мощностей в различных дифракционных порядках.
Решение. Взяв в качестве исходного выражения пространственный спектр амплитудной дифракционной решетки (1.27), вычислим интегралы по переменной x для каждого из дифракционных порядков.
Нулевой порядок:
(1.33)
Первый порядок:
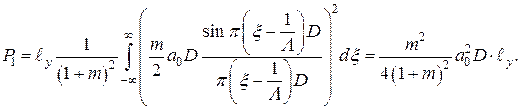(1.34)
Первый отрицательный порядок:
(1.35)
Как видно из расчетов, при максимальной глубине модуляции т = 1 суммарная мощность всех порядков дифракционного излучения составляет
Полная мощность, падающая на дифракционную решетку, равна 
. Остальная мощность, т.е. 
, поглощается в амплитудной гармонической решетке. Отражение излучения при расчетах полагалось равным нулю.
Равенство Парсеваля здесь должно выполняться только в пространстве справа от амплитудной решетки. Проверим это. Проинтегрируем по координате х распределение мощности излучения, прошедшего через решетку. Для упрощения вычислений положим, что в апертуре D укладывается целое число периодов решетки, при этом интегралы от функций 
и 
равны нулю.
При максимальной глубине модуляции т = 1 имеем:
(1.36)
Таким образом, мы показали, что прошедшая мощность и суммарная мощность всех компонент пространственного спектра равны, равенство Парсеваля выполняется.
Интересно по результатам этих расчетов оценить эффективность амплитудной дифракционной решетки. Эффективностью дифракционной решетки принято называть отношение мощности оптического пучка в первом дифракционном порядке, к полной падающей мощности дифракционного пучка.
(1.37)
Из (1.34) и (1.31) при т = 1 получим величину h = 1/16 = 6,25%.
Как видно, амплитудная решетка характеризуется довольно низкой эффективностью дифракции.
Поиск по сайту: