Плоская волна

Российский университет дружбы народов

В.А. Комоцкий

КОГЕРЕНТНАЯ ОПТИКА И ГОЛОГРАФИЯ

Конспект лекций

Москва

Г.

Курс лекций «Когерентная оптика и голография» предназначен для студентов старших курсов специальности «Радиофизика и электроника». Рекомендуется изучать материал этого курса после изучения курса математического анализа и классического курса оптики.

В первом разделе рассмотрено представление оптического сигнала в виде пространственного спектра, анализируются пространственные спектры при дифракции оптической волны на амплитудных и фазовых периодических дифракционных решетках, пеобразование модуляции волнового фронта при движении волны в пространстве. Проведены оценки эффективности дифракции.

Во втором разделе рассмотрена задача интерференции двух плоских волн, кратко описан принцип интерферометрии. Обсуждается понятие когерентности волн, рассмотрена связь когерентности с шириной спектральной линии и с контрастом интерференционной картины.

В третьем разделе дано краткое описание дифракционного интеграла, его применения для анализа системы транспарант - тонкая линза. Рассмотрены практические схемы пространственной фильтрации и фазового контраста, некоторые схемы оптической обработки сигналов.

В четвертом разделе изложены основные принципы голографии на основе анализа схемы с наклонным опорным пучком. Рассмотрена схема Фурье голографии, а также простейшая схема распознавания образов.

Данный конспект следует рассматривать как некоторую начальную ступень, которая поможет преодолеть трудности при дальнейшем углубленном изучении специальной литературы, статей, монографий в областях науки, связанных с когерентной оптикой и голографией.

Раздел I

ПРОСТРАНСТВЕННЫЕ СПЕКТРЫ

И ПРОСТРАНСТВЕННЫЕ ЧАСТОТЫ

Плоская волна

При исследовании распространения и дифракции когерентных световых волн нередко пользуются моделью плоской электромагнитной волны. Плоская волна − это простейшая когерентная волна. Она может быть описана следующим выражением:

. (1.1)

где 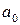− амплитуда волны; − круговая частота световых колебаний,

f - частота световых колебаний, − волновой вектор; − компоненты волнового вектора по направлениям координат x, y, z. Модуль волнового вектора , где l − длина волны когерентного света.

Следует заметить, что в выражении (1.1) амплитуда волны записана как скалярная величина, в то время как обычно в электродинамике амплитуду волны выражают через напряженность поля − величину векторную. Скалярная запись зачастую используется при анализе тех систем когерентной оптики, в которых распространение света происходит в изотропной среде и поляризация света при прохождении волны через оптическую систему не меняется.

Практически при записи уравнений плоской волны обычно опускают множитель и оперируют с той частью формулы (1.1), которая не зависит от времени, , и эту часть называют в литературе " комплексная амплитуда ". Если же рассматривать какую-либо плоскость оптической системы, например, плоскость z = 0, то для определения направления движения плоской волны достаточно записать ее уравнение в виде:

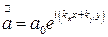, (1.2)

отбросив множитель . При этом информация о величине не теряется, поскольку можно выразить через величины: .

Компоненты вектора выражаются следующими формулами:

. (1.3)

Здесь 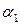− угол между вектором и осью Оx; − угол между вектором и осью Оy; а углы q ₁ и q ₂ соответственно равны: ; 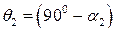. Величины

и (1.4)

называют пространственными частотами по координатам х и у.

Рис 1.1. Характеристики плоской волны. Справа- иллюстрация зависимости фазовой задержки от направления волны.

Соотношения, записанные выше, иллюстрируются рисунком 1.1, где изображены следы волновых поверхностей плоской волны. Для наглядности на этом рисунке изображен частный случай, когда волновой вектор лежит в плоскости x0z. В этом частном случае комплексная амплитуда плоской волны, падающей под углом 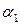к оси 0х и под углом = 90⁰ к оси 0у, может быть записана

. (1.5)

В этой записи мы положили z = 0 (сравните с формулой (1.1)) и тем самым ограничили действие формулы (1.4) только плоскостью z = 0. Если возникает необходимость найти распределение амплитуд и фаз в другой плоскости 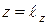, то выражение (1.5) следует дополнительно умножить на

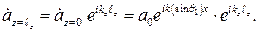(1.6)

Величину можно выразить через и другие компоненты и , используя соотношение . Отсюда имеем выражение:

(1.7)

в частности для случая

.

Нередко в литературе пользуются формулами, выраженными не через углы a, а через дополнительные углы . Тогда

. (1.8)

Если плоская волна прошла в свободном пространстве путь от плоскости z = 0 до плоскости , то она преобразуется следующим образом:

(1.9)

экспоненциальный множитель выражает фазовую задержку, которую испытывает плоская волна, когда она проходит от плоскости z = 0 до плоскости .

Интересно заметить, что фазовая задержка максимальна, когда волна распространяется в направлении оси 0 z. В этом случае , , 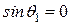. Если угол наклона направления движения волны по отношению к оси z увеличивается, то, как следует из формулы (1.9), фазовая задержка волны уменьшается. Это иллюстрируется двумя картинками справа на рис. 1.1.

1.2. Прохождение плоской волны через транспарант

При анализе оптических систем мы нередко встречаемся с разнообразными оптическими объектами, которые имеют очень малую протяженность в направлении оптической оси 0 z. Подобные объекты называются транспарантами. К таким объектам можно отнести, например, дифракционные решетки, изображения объектов, текстов, рисунков, записанные на фотопластинке. К классу плоских транспарантов относятся также некоторые виды голограмм. В общем случае подобные объекты могут изменять как амплитуду, так и фазу световой волны, проходящей через объект. В отдельных случаях может изменяться только амплитуда или только фаза световой волны. В первом случае транспарант называют амплитудным, а во втором случае − фазовым транспарантом. К числу фазовых транспарантов можно отнести фазовую дифракционную решетку, тонкую линзу и другие тонкие объекты, не поглощающие св ет.

Итак, транспарант характеризуется комплексной функцией прозрачности , зависящей от двух координат в плоскости . Если слева на транспарант падает плоская волна с амплитудой 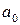, направленная вдоль оси z, то справа от транспаранта в плоскости на бесконечно малом расстоянии от плоскости распределение амплитуд определяется произведением:

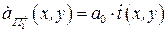. (1.10)

Таким образом, справа от плоскости транспаранта получим неоднородную волну, амплитуда и фаза которой зависят от координат х и у. После прохождения транспаранта оптическая волна получает пространственную модуляцию. Таким образом, оптическая волна после прохождения транспаранта может нести на себе некоторый оптический сигнал в виде пространственной модуляции волнового фронта. Модуляция может быть амплитудной, фазовой, а также сложной амплитудно-фазовой. Оптические сигналы можно обрабатывать (подобно радиотехническим сигналам). Так, например, можно проводить операции фильтрации. В отличие от радиотехнических сигналов оптические сигналы могут быть двумерными, т.е. описываются функциями двух переменных. Подобно тому, как при анализе радиотехнических сигналов используется представление сигнала в виде спектра, при анализе оптических сигналов применяется представление оптического сигнала, т.е. оптической волны с пространственной фазовой модуляцией, в виде пространственного спектра, который находят с помощью преобразования Фурье.

Поиск по сайту: