Пространственная фильтрация с применением фазового фильтра. Метод фазового контраста

При решении некоторых практических задач представляет интерес наблюдение и исследование фазовых объектов, у которых полезная информация заключена в пространственной фазовой модуляции транспаранта. Фазовая пространственная модуляция практически неразличима глазом при простом непосредственном наблюдении. Метод фазового контраста позволяет преобразовать фазовую модуляцию в амплитудную, которую легко можно наблюдать визуально. Оптическая схема, реализующая метод фазового контраста изображена на рис. 3.6

Рис.3.6. Схема пространственной фильтрации по методу фазового контраста.

Фазовый транспарант можно описать функцией вида:

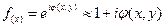(3.35)

Будем рассматривать эту задачу в приближении малой глубины фазовой модуляции, при этом можно записать: . С помощью первой линзы в оптической схеме выполняется преобразование Фурье при переходе из плоскости первой линзы к ее фокальной плоскости. Преобразование Фурье функции 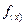будет иметь вид:

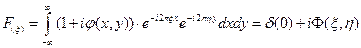(3.36)

Здесь функция 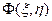является Фурье преобразованием функции модуляции 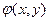. В плоскости пространственных частот функция 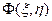распределена в широком диапазоне координат этой плоскости. В то же время функция 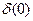сосредоточена в узкой области нулевых координат фокальной плоскости.

Пространственный фильтр представляет собой прозрачную пластинку, в центральной части которой создано утолщение (а возможно и углубление), которое создает дополнительный фазовый сдвиг проходящей оптической волны на по отношению ко всей остальной пластине. Напомним, что . Если отбросить постоянный фазовый сдвиг в прозрачной пластине, то воздействие фильтра на комплексную волну в фокальной плоскости выражается следующими операциями. В выражении (3.36) первое слагаемое следует умножить на ,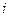

а второе слагаемое следует умножить на 1. В результате выражение, описывающее пространственный спектр на выходе фильтра примет вид:

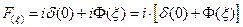(3.37)

Вторая линза выполняет обратное Фурье преобразование. В результате на выходе мы получаем следующее распределение:

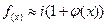(3.38)

Отбросив постоянный фазовый сдвиг на 90 градусов (т.е. 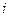) на всей плоскости, мы видим, что функция представляет собой амплитудную модуляцию. В этом можно убедиться также, если найти распределение интенсивности, помножив выражение (3.38) на комплексно сопряженное выражение.

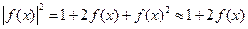(3.39)

В результате мы показали, что рассмотренная здесь оптическая схема преобразует фазовую модуляцию в амплитудную. Схему можно применить для наблюдения и исследования фазовых, например биологических объектов.

3.6 Акустооптические схемы с линзами, предназначенные для оптической обработки радиосигналов.

3.6.1. Вводные замечания. Рассмотрим здесь две акустооптические схемы обработки радиосигналов, которые могут выполнять операцию анализа спектра и операцию свертки радиосигналов. Эти схемы обычно включают в себя три важных компонента.

· Пространственный модулятор когерентной световой волны, который преобразует функцию, описывающую радиосигнал, в соответствующую ей функцию пространственной модуляции волнового фронта световой волны. Эту функцию выполняет акустооптическая ячейка.

· Линза, выполняющая преобразование Фурье оптического сигнала;

· Фотодиод или набор (линейка) фотодиодов, которые преобразуют оптический сигнал в электрический сигнал на выходе схемы.

Пространственный модулятор. В качестве пространственного модулятора применяется акустооптическая (А.О.) ячейка. На рис 3.7 изображена схема А.О. ячейки, в которой используется эффект дифракции света на акустической (ультразвуковой) волне, т.е. схема дифракции Рамана-Ната. Возбудитель 1 представляет собой пластину, вырезанную из кристалла, обладающего пьезоэлектрическим эффектом или пластину из пьезокерамики. На обеих сторонах пластины нанесены металлические электроды. Возбудитель плотно связан со звукопроводом с помощью слоя индия или с помощью специального клея. Радиосигнал подается на электроды возбудителя ультразвуковых колебаний. Несущая частота радиосигнала находится в области резонанса механических колебаний возбудителя. При этом относительная ширина полосы частот возбудителя обычно велика, так как возбудитель сильно нагружен, и при этом значительная доля энергии колебаний передается в звукопровод. Колебания пластины возбуждают в звукопроводе бегущую со скоростью V акустическую волну. На противоположном конце звукопровода располагается поглотитель акустической волны, чтобы предотвратить помехи, которые может вызвать волна, отраженная от торца звукопровода.

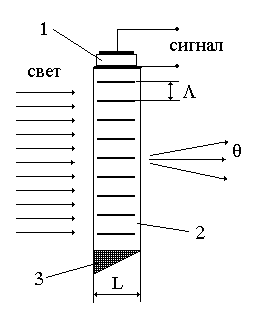
Рис.3.7. Схема акустооптической ячейки, работающей в режиме

Рамана-Ната. 1- пьезоэлектрический возбудитель ультразвуковой волны,

2- звукопровод, 3-поглотитель ультразвуковой волны.

В результате прохождения через акустооптическую ячейку когерентная оптическая волна с длиной волны получает пространственную фазовую модуляцию в соответствии с радиосигналом, который подан на электроды возбудителя. Так, например, если сигнал имеет вид:

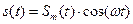, (3.40)

то выражение, описывающее пространственную фазовую модуляцию волнового фронта оптической волны на выходе акустооптической ячейки, работающего в режиме Рамана-Ната, имеет вид:

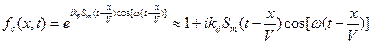(3.41)

Здесь 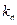- коэффициент, связывающий возмущения фазы волнового фронта с амплитудой сигнала.

Напомним, что режим Рамана-Ната имеет место при условии: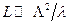

В выражении (3.41) мы использовали приближение малой амплитуды пространственной фазовой модуляции волнового фронта, вызванной акустической волной, так как при малых глубинах модуляции схема находится в линейном режиме. При малой амплитуде фазовой модуляции каждой частоте радиосигнала будет соответствовать определенный набор пространственных частот пространственного спектра и определенные углы направления дифракции первых порядков:

(3.42)

3.6.2.Схема акустооптического анализатора спектра радиосигналов.

Рис.3.8. Схема акустооптического анализатора спектра радиосигналов.

Положим, что в схеме акустооптического анализатора спектра, которая изображена на рис.3.8, на вход возбудителя подан монохроматический радиосигнал с частотой . В звукопроводе возбуждается акустическая волна с длиной волны . В результате формируется дифрагированная оптическая волна, направленная под углом :

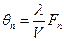(3.43)

Эта волна дает отклик на плоскости 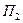в виде дифракционного пятна в точке с координатой, которую в приближении малых углов дифракции можно выразить формулой:

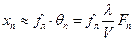(3.44)

Каждой частоте соответствует точка 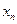на плоскости 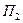. В этих точках расположены фотодетекторы, и с выхода каждого из фотодетекторов снимают электрический сигнал, соответствующий частоте .

Оценим предельную разрешающую способность данного анализатора. Размер дифракционного фокального пятна можно оценить как

(3.45)

Здесь D- поперечный размер оптического пучка, k- коэффициент который может быть порядка 1.

При практическом конструировании схемы желательно, чтобы размер фокального пятна и размер фотодетектора совпадали. Положим, что расстояние между соседними фотодетекторами составляет величину порядка размера фокального пятна, . Тогда, взяв дифференциал 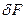из (3.44) и приравняв , с учетом (3.45) можно получить:

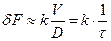(3.46)

Здесь 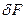- разрешающая способность анализатора, 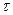- время прохождения акустической волны через апертуру оптического пучка.

Проведем простую количественную оценку. Пусть в качестве материала звукопровода выбран плавленый кварц. Скорость распространения продольной звуковой волны составляет 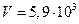м/c. При размере апертуры D=1см, 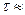1,6 мкс и при k=1,22 получим .

Важным параметром устройства является число разрешаемых точек в пределах рабочего диапазона. Диапазон частот, в котором может работать данная схема, ограничена полосой частот возбудителя акустических волн. Полоса частот составляет некоторую долю, возможно, порядка 20-30% от центральной резонансной частоты. Зная можно оценить число разрешаемых точек N:

(3.47)

Если 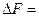60мГц, а 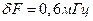, то число N=100. В последней формуле можно подставить полосу в мегагерцах, а длительность в микросекундах.

Важной особенностью схемы акустооптического анализатора спектра радиосигналов является очень малое время, необходимое для получения результатов. Практически оно составляет величину порядка 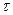, т.е. порядка времени прохода акустической волны через звукопровод. В подобных случаях принят термин: «анализ в реальном масштабе времени».

3.6.3 Схема, выполняющая операцию свертки двух радиосигналов (конвольвер) изображена на рис. 3.9..

Рис.3.9. Схема акустооптического конвольвера (схема Ван дер Люгта).

Имеются два сигнала.

Сигнал1 (входной):

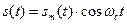(3.48)

Сигнал 2 (опорный):

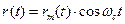(3.49)

Здесь 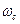- несущая частота сигналов. 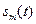и 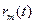- функции модуляции сигналов, т.е. огибающие несущей частоты.

В результате обработки этих сигналов схемой 3.9 можно получить функцию свертки данных сигналов, или их огибающих, т.е. функцию вида:

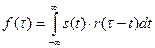(3.50)

Следует заметить, что операция свертки во временной области для некоторого класса сигналов соответствует операции оптимальной фильтрации в частотной области. В общем случае для оптимальной фильтрации сигнала необходимо произвести операцию корелляции его с опорным сигналом.

Схема конвольвера, изображенная на рис 3.9, выполняет задачу получения на выходе схемы некоторого электрического сигнала, пропорционального свертке двух входных сигналов, поданных на акустооптические ячейки.

Схема содержит две акустооптические ячейки, которые расположены последовательно по ходу оптического пучка, просвечивающего систему. Радиосигналы 1 и 2 вводятся в акустооптические ячейки, где распространяются в виде волн, бегущих со скоростью V в противоположных направлениях:

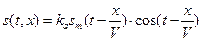, (3.51)

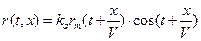. (3.52)

Здесь - коэффициент, связывающий возмущения в звукопроводе с амплитудой сигнала. После прохождения двух пространственных модуляторов оптическая волна получает фазовую модуляцию:

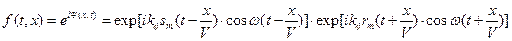(3.53)

Здесь 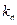- коэффициент, связывающий возмущения фазы волнового фронта с амплитудой сигнала.

Если фазовая модуляция волнового фронта неглубока, 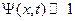, то , а функцию модуляции можно представить:

(3.54)

Далее линза 1 выполняет преобразование Фурье функции .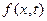

Первое слагаемое 1 дает в Фурье плоскости 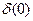. Эта часть спектра задерживается пространственным фильтром, его центральной частью.

Пространственные спектры функци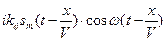й и 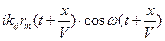лежат в областях пространственных частот и в плоскости пространственного фильтра проходят через отверстия в пространственном фильтре. После прохождения пространственного фильтра вторая линза (линза2) выполняет обратное преобразование Фурье. В плоскости фотодетектора мы получаем сумму амплитуд: 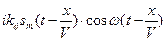+ 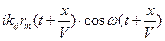. Далее фотодетектор с большой площадью интегрирует весь приходящий сигнал и выдает на выходе электрический сигнал, пропорциональный интегралу от интенсивности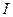 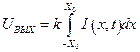. Заменим 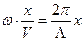, с учетом этого функция интенсивности имеет вид:

(3.55)

В результате интегрирования два первых слагаемых дают постоянную составляющую. В третьем члене выражения (3.55) мы заменим произведение косинусов суммой косинусов:

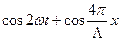(3.56)

При интегрировании второго члена по переменной x в пределах значительно превышающих длину акустической волны 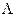, получим 0. С учетом этого в результате интегрирования третьего слагаемого выражения 3.55 получим следующий ненулевой результат:

(3.57)

Если сигнал с выхода фотодетектора пропустить через полосовой фильтр с центральной частотой 2 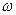, то на выходе получим функцию, типа свертки, наложенную на удвоенную несущую частоту. Формально интеграл отличается от функции свертки только пределами интегрирования. В интеграле 3.57 пределы интегрирования определяются размерами фотодетектора .

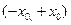За пределами этого интервала сигнал равен 0, поэтому формально мы можем расширить область интегрирования до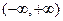

Мы рассмотрели две акустооптические схемы, в которых на вход подаются радиосигналы, с выхода получают электрические сигналы, а внутри схемы используются акустические и световые волны. В результате мы получили новое качество: очень малое время обработки сигналов.

Поиск по сайту: