Пространственный спектр в случае дифракции оптической волны на амплитудной щелевой решетке

Рассмотрим плоскую дифракционную решетку, образованную периодически чередующимися прозрачными и непрозрачными полосками (рис.1.16). Макет решетки такого типа легко изготовить в лаборатории путем фотографирования на фотопластинку чертежа решетки.

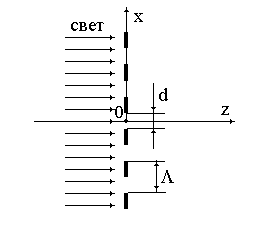
Рис. 1.16. Прохождение когерентного света через амплитудную щелевую решетку.

Рассмотрим решетку бесконечных размеров. Функцию пропускания в пределах периода можно описать следующим выражением:

T (x)=1 при

T (x)=0 при и (1.113)

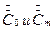Представим функцию пропускания в виде ряда Фурье вида (1.94) . Коэффициенты вычисляем по формулам (1.95) и (1.96). В результате получим:

, (1.113)

В том случае, если ширина щели d равна половине периода решетки, коэффициенты разложения в ряд следующие:

, , , , , ….. (1.114)

Если световая волна с амплитудой направлена вдоль оси 0z, т.е. по нормали к поверхности решетки, то пространственный спектр дифрагированных волн будет иметь вид подобный формуле (1.100)

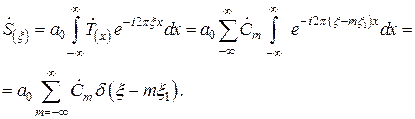
Коэффициенты при этом определены выражением (1.113).

Поиск по сайту: