Интерференция двух плоских волн

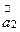Рассмотрим следующую простую задачу. На экран, расположенный в плоскости х0у, падают две плоские когерентные оптические волны: и . Векторы напряженности электрических полей (векторы поляризации) этих волн параллельны между собой и параллельны оси 0у. Волновые векторы и этих волн лежат в плоскости х0z и направлены симметрично относительно оси 0z под углами + q и - q к оси 0z (Рис 2.1).

Рис 2.1. Схема ля анализа интерференции двух плоских волн.

Запишем уравнения плоских волн в виде:

. (2.1)

Здесь - амплитуда волны; j - некоторая начальная фаза,

В данном случае проекции волновых векторов 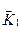и на ось 0x равны:

. (2.2)

(2.3)

Здесь , - пространственная частота волны по координате 0х, l - длина волны света..

В области интерференции, на плоскости х0у при z = 0, можно записать следующие выражения для комплексных амплитуд волн и :

, (2.4)

. (2.5)

Здесь и некоторые начальные фазы интерферирующих волн.

Суммарное поле волн в плоскости х0у равно:

. (2.6)

Следует напомнить, что при измерениях в оптике приборы регистрируют не амплитуду волны, а ее интенсивность, т.е. величину, пропорциональную плотности мощности излучения. Интенсивность определяют лак , и она равна произведению комплексной амплитуды на комплексно сопряженную величину. Найдем распределение интенсивностей в области интерференции, используя выражение (2.6) и формулу .

. (2.7)

. (2.8)

Перемножив (2.7) и (2.8), получим:

(2.9)

Здесь 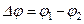- разность фаз двух когерентных волн в точке начала координат х = 0, z = 0.

Анализ выражения (2.9) приводит к следующим выводам.

· В области интерференции на плоскости х0у имеют место периодические изменения интенсивности с периодом интерференции , который можно найти из соотношения . Отсюда получим:

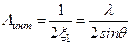. (2.10)

· Условие соответствует расположению начала координат

х = 0 в точке максимума распределения интенсивности интерференционной картины, наблюдаемой на плоскости х0у.

· Расположим начало отсчета координаты x в максимуме интерференционной картины. Это будет соответствовать начальному сдвигу фаз . Если затем на пути одной из волн, участвующих в интерференции, ввести возмущение показателя преломления среды, приводящее к сдвигу фазы волны на величину , то интерференционная картина сдвинется относительно выбранной системы координат на величину , которую можно определить из соотношения , т.е. приравняв нулю новый аргумент косинуса. В результате находим:

. (2.11)

С учетом (2.10) соотношение (2.11) можно переписать в виде:

, (2.12)

а также выразить в виде следующей пропорции:

. (2.13)

Итак, из выражения 2.13 следует, что дополнительный сдвиг фазы одной из интерферирующих волн вызывает сдвиг интерференционной картины, который в отношении к периоду этой интерференционной картины составляет долю, равную отношению величины дополнительного фазового сдвига, внесенного на пути оптической волны к величине 2 p.

Коэффициент, характеризующий видность интерференционной картины, (коэффициент контраста) обычно характеризуют следующим отношением:

. (2.14)

В том случае, когда амплитуды интерферирующих волн одинаковы, этот коэффициент равен 1. Как видно из выражения (2.9), при условии, что амплитуды волн одинаковы, интенсивность интерференционной картины при изменении координаты x изменяется в пределах от величины до величины . Следует подчеркнуть, что нулевая интенсивность в минимумах будет наблюдаться только в том случае, если амплитуды когерентных интерферирующих волн равны. Если же амплитуды интерферирующих волн различны, то интенсивность в минимуме не равна нулю, , а видность интерференционной картины будет меньше единицы.

Для того чтобы убедиться в этом, проведем простой расчет. Пусть

, (2.15)

.

Для упрощения здесь мы положили . Тогда получим:

. (2.16)

При условии, что 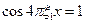получим значение максимальной интенсивности в дифракционной картине:

(2.17)

При условии, что получим значение минимальной интенсивности в дифракционной картине:

(2.18)

Если , то коэффициент видности будет меньше 1. При этом любая из этих амплитуд может быть больше другой, это не имеет значения.

. Рассмотрим пример 1.

Пусть , , 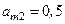тогда проведя расчет по формуле 2.16 получим:

,

,

,

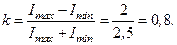
Пример 2. Пусть , .

.

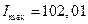
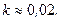
Таким образом, видность интерференционной картины снижается при увеличении разницы между амплитудами интерферирующих волн.

Поиск по сайту: