Запись голограмм и восстановление волнового фронта

4.1.1 Введение. Голография это особый, специфический метод записи оптической волны и последующего ее восстановления. Для записи голограмм используют специальные чувствительные к свету материалы, которые получили название фоточувствительные среды для записи голограмм. В частности, для записи голограмм широко применяются фотопластинки, изготовленные по специальной технологии и имеющие очень высокую разрешающую способность записи, порядка нескольких тысяч линий на миллиметр.

Специфика голографической записи состоит в том, что на фоточувствительную среду записывают не изображение, а интерференционную картину от двух волн. Одна из этих волн исходит от объекта. Эту волну обычно называют объектной, или предметной, или сигнальной волной. Она содержит оптический сигнал и образуется в результате взаимодействия когерентной волны с объектом. Объектом может быть любой предмет, либо частично прозрачная плоская картина, которую в этом случае называют транспарантом.

Вторая волна – опорная. Она формируется из излучения того же когерентного источника, который освещает объект. С этой целью при проведении записи голограммы пучок излучения лазера разделяют на два оптических пучка, один из которых будет опорным, а второй после взаимодействия с объектом будет сигнальным. В качестве опорной волны часто используют волну с плоским волновым фронтом или сферическую волну. Простая форма волнового фронта в значительной степени упрощает процесс последующего восстановления изображения. В некоторых схемах записи голограмм отсутствуют специальные устройства для разделения волн. Так, например, в схеме Габора в качестве опорной волны используется часть волны, освещающей частично прозрачный объект, которая проходит через достаточно обширные прозрачные области объекта.

Записанную на голограмме сигнальную волну можно восстановить, если облучить голограмму опорной волной. В восстановленной оптической волне сохраняется форма амплитудного и фазового распределения волны. Восстановленное с голограммы изображение предмета выглядит объемным.

Впервые принцип голографии был сформулирован американским ученым Д. Габором в 1948 году (D. Gabor, Nature, 149, 777, 1948). Вскоре им были изготовлены первые голограммы, которые демонстрировали принципиальную возможность записи и восстановления голограммы. В 1952 году Роджерс опубликовал сообщение о результатах экспериментальных исследований оптической голографии, выполненных с применением ртутной дуговой лампы в качестве источника излучения: (G. L. Rogers, Proc. Roy. Soc. 63A, 193, 1952). Однако, ввиду отсутствия в то время источников света с высокой степенью когерентности возможности практического применения голографии были ограничены. Новый этап развития голографии наступил после изобретения лазеров - источников света с высокой степенью когерентности. Были предложены новые схемы записи и восстановления голограмм, отличные от схемы Д. Габора. Некоторые из этих схем мы рассмотрим ниже

4.1.2. Схема записи голограммы с наклонным опорным пучком ( рис.4.1. ).

Рис.4.1. Схема записи голограммы с наклонным опорным пучком. Вариант схемы с плоским прозрачным объектом − транспарантом.

Эта схема была предложена исследователями из США Лейтом и Упатниексом (Leith E.N., Upatnieks J., J. Optical Society of America, v. 52, р.1123, 1962г.). В схеме для освещения объекта и для создания опорной волны используется когерентная волна с плоским волновым фронтом, которая разделяется на две части. Верхняя оптического пучка часть идет на освещение объекта (предметная волна), а другая часть пучка− на создание опорнойволны. В схеме на рис.4.1 голографируемый объект представляет собой плоский прозрачный транспарант, который просвечивается когерентной волной от лазера. Опорная волна формируется из нижней части оптического пучка и направляется на голограмму под углом к оси 0z. Наклон волны создается за счет введения преломляющей призмы в эту часть оптического пучка. При теоретическом анализе мы будем считать опорную волну плоской волной.

Если объект непрозрачен, и его нельзя просветить насквозь, следует несколько видоизменить схему и использовать отраженную от объекта волну. Этот вариант показан на рис. 4.2. В этой схеме нужное направление опорной волны создается за счет наклона отражающего зеркала.

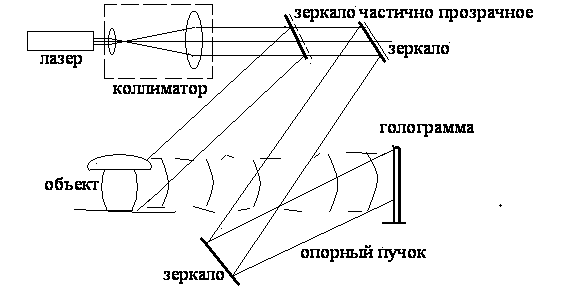
Рис.4.2. Схема записи голограммы непрозрачного объекта с наклонным опорным пучком. Коллиматор, состоящий из двух линз, служит для расширения лазерного пучка до необходимого поперечного размера. Частично прозрачное зеркало разделяет лазерный пучок на два: опорный и сигнальный.

Уравнение плоской опорной волны можно записать:

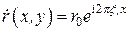, (4.1)

где 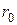− амплитуда опорной волны; − пространственная частота опорной волны.

Пространственный спектр плоской опорной волны имеет вид d -функции:

. (4.2)

Предметная волна. После того как плоская волна прошла через транспарант, она получила пространственную модуляцию волнового фронта и больше не является плоской волной. Распределение амплитуд и фаз предметной волны непосредственно за транспарантом можно описать некоторой комплексной функцией 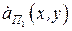, а в плоскости голограммы – функцией .

4.1.3. Запись голограммы. В плоскости голограммы происходит интерференция опорной и предметной волн. Суммарное распределение амплитуд в плоскости голограммы имеет вид:

. (4.3)

В этом выражении − комплексное распределение амплитуд предметной волны в плоскости голограммы . Комплексно сопряженную волну будем обозначать 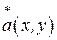. Найдем распределение интенсивностей в плоскости голограммы:

. (4.4)

Для записи голограмм обычно используют фотопластинки. Функция прозрачности (функция пропускания) фотопластинки t(x,y) изменяется в соответствии с распределением интенсивности . Прозрачность фотопластинки уменьшается с увеличением плотности энергии экспозиции, которую мы определим как произведение интенсивности излучения на длительность экспозиции 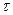. Вид зависимост и прозрачности пластинки от плотности энергии экспозиции изображен на рис. 4.3.

Рис 4.3. Вид зависимости прозрачности фотопластинки t от величины плотности энергии экспозиции .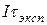

На этой зависимости можно выделить линейный участок, который можно аппроксимировать следующей формулой:

. (4.5)

Здесь , − коэффициенты смещения и наклона линейного участка, определяемые из экспериментальной характеристики фотопластинки.

С учетом соотношений (4.4), (4.5) можно записать распределение функции прозрачности фотопластинки после записи на ней голограммы, т.е. после проявления экспонированной фотопластинки:

. (4.6)

На этом описание этапа записи голограммы заканчивается. Далее рассмотрим, как восстанавливается изображение с полученной голограммы.

4.1.3. Восстановление оптической волны. Для восстановления оптической волны с записанной голограммы мы осветим ее тем же наклонным опорным пучком, с помощью которого производилась запись голограммы. Транспарант мы удалим, а также удалим и оптическую волну, освещавшую транспарант. Расположение голограммы и опорного пучка сохраним.

Рис. 4.4. Схема восстановления оптической волны при освещении голограммы

опорной волной.

Опорная волна пройдет через голограмму с функцией пропускания . В результате справа от голограммы получим распределение амплитуд , которое можно выразить как произведение функции опорной волны на функцию прозрачности голограммы:

−

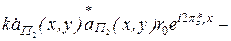
. (4.7)

В полученном выражении (4.7) присутствует слагаемое (четвертое)

− . Оно с точностью до постоянного множителя повторяет функцию , которая описывает волну от исходного объекта. Знак минус указывает, что фаза этой волны сдвинута на 180⁰ по отношению к исходной волне. Это слагаемое описывает восстановленную предметную волну. Форма ее волнового фронта повторяет все особенности формы волнового фронта, исходящего от реального объекта. Если наблюдатель будет рассматривать эту волну справа от голограммы, то он будет наблюдать объемное изображение объекта в той же области пространства, где объект находился ранее, когда производилась запись голограммы. Поскольку это наблюдаемое изображение объекта находится слева от голограммы, а восстановленная волна от него существует только справа от голограммы, то такое изображение называют мнимым, по аналогии с мнимым изображением предмета в зеркале. В принципе, если есть необходимость, то это мнимое изображение можно перевести в действительное, воспользовавшись выпуклой линзой или объективом фотоаппарата. Например, можно сфотографировать восстановленное изображение предмета на фотопленку с помощью обычного фотоаппарата, или на матрицу цифрового фотоаппарата по схеме показанной на Рис4.5. В отличие от восстановленного голографического изображения его фотография не будет передавать объемную фактуру изображения.

Рис.4. 5. Схема, поясняющая, как с помощью линзы преобразовать мнимое

изображение, восстановленное голограммой, в действительное изображение.

Перейдем к обсуждению роли других слагаемых формулы (4.7). Волны, описываемые первым, вторым и третьим, а также пятым слагаемыми выражения (4.7), не используются при наблюдении мнимого изображения а, напротив, могут создавать помехи при его наблюдении.

Первое и второе слагаемые имеют вид плоских волн, форма которых с точностью до постоянного множителя повторяет форму опорной волны.

Третье слагаемое это волна, имеющая несущую пространственную частоту, равную 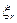, на которую наложена пространственная модуляция вида

Пятое слагаемое представляет собой комплексно сопряженную волну 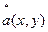, которая модулирует несущую волну , имеющую пространственную частоту, равную 2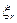

Для обсуждения условий, при которых возможно наблюдение восстановленного с голограммы мнимого изображения без помех, создаваемых другими восстановленными волнами, мы более детально проанализируем пространственный спектр восстановленных волн за голограммой.

4.1.4. Анализ пространственного спектра восстановленных волн

Выполним Фурье-преобразование выражения (4.7) и будем анализировать полученное выражение, описывающее пространственный спектр восстановленных волн. Ввиду того, что множитель в (4.7) одинаков для всех членов, мы не будем записывать его в дальнейшем. Картина распределения амплитуд пространственного спектра волн после голограмм изображена на рис.4.6

Рис 4.6.Пространственный спектр восстановленных волн от голограммы, построенный в соответствии с выражением (4.7).

Первое слагаемое в выражении (4.7) восстановленной волны − это "остаток" плоской опорной волны, прошедшей через голограмму. Фурье-преобразование (спектр) этого слагаемого имеет вид дельта функции:

. (4.8)

Аналогичный вид имеет Фурье-преобразование второго слагаемого:

. (4.9)

Эти составляющие пространственного спектра изображены на рис.4.6 в виде вертикальных стрелок.

Пространственный спектр восстановленной волны 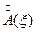соответствует четвертому члену в выражении 4.7. Функция 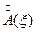является Фурье преобразованием функции .

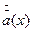. (4.10)

Положим, что 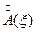занимает участок пространственного спектра от частоты до в районе нулевой пространственной частоты. На рисунке 4.6. он изображен в форме прямоугольника и соответствует пространственному спектру волны, исходящей от предмета.

Пространственный спектр сопряженной волны (соответствует пятому слагаемому в выражении 4.7) занимает участок в районе пространственной частоты от частоты до частоты 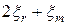. Для доказательства этого рассмотрим выражение пятого слагаемого (4.7):

(4.11)

и найдем Фурье образ (4.11), выразив его через известный нам Фурье образ . Для простоты рассмотрим функцию одной переменной . Пусть имеет Фурье преобразование

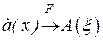, т.е. 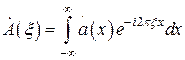. (4.12)

Выразим Фурье преобразование сопряженной функции

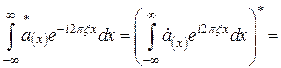
. (4.13)

Значок * здесь означает сопряжение.

. (4.14)

Таким образом, показано каким способом Фурье образ сопряженной функции можно выразить через Фурье образ функции :

если , (4.15)

то .

Операция сопряжения и оборота оси координат (замена x на - x) не изменяют ширины спектра. В нашем простейшем случае конфигурация спектра (форма прямоугольника) сохраняется. Однако в выражении (4.11) кроме величины и постоянного множителя присутствует множитель 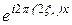. Известно, что умножение функции на экспоненциальный множитель такого вида приводит к сдвигу1⁾ спектра этой функции. В данном случае пространственный спектр сдвинут на величину по оси частот. В результате функция будет иметь Фурье образ вида:

. (4.16)

Формулу (4.16) можно получить и другим путем:

(4.20)

Таким образом, на шкале пространственных частот диаграмма пространственного спектра сопряженной волны изображается прямоугольником с протяженностью с центром на пространственной частоте .

Исследование формы пространственного спектра третьего члена выражения (4.7), который имеет вид , дает следующую картину. Форма этого спектра имеет вид автокорелляции функции , и эта функция сдвинута на величину относительно точки начала координат .

Если спектр сигнала имеет форму прямоугольника (рис. 4.6), то спектр третьего слагаемого имеет форму симметричного равнобедренного треугольника, ось симметрии которого проходит через точку . Спектр занимает полосу пространственных частот от 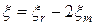до , и имеет ширину . Вывод выражения, которое определяет форму спектра третьего слагаемого, приведен ниже.

Некоторые определения и формулы.

Преобразование Фурье функции имеет вид:

, (4.21)

обратное преобразование Фурье:

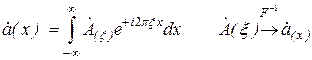, (4.22)

свертку двух функций определяют формулой:

. (4.23)

Функцию корелляции двух функций определяют формулой:

. (4.24)

Если функция тождественна функции , то операция корелляции называется операцией автокорелляции:

. (4.25)

Анализ формулы третьего слагаемого выражения (1.7)

Запишем Фурье-интеграл от функции

, (4.26)

а затем функцию заменим ее обратным Фурье преобразованием и изменим порядок интегрирования:

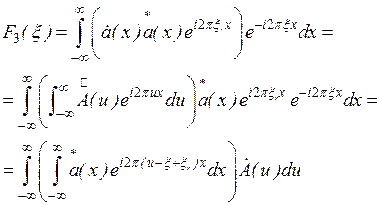(4.27)

Преобразуем интеграл, стоящий в скобках:

(4.28)

Подставив полученное выражение (4.28) в (4.27), получим:

. (4.29)

Можно провести замену переменных:

. (4.30)

Затем следует привести формулу (П₉) к виду, подобному (П₅):

. (4.31)

Отсюда видно, что спектр функции равен функции автокорелляции функции , сдвинутой относительно начала координат на величину .

Поиск по сайту: