Пространственный спектр

Как известно из математического анализа, функцию или , удовлетворяющую условию абсолютной (квадратичной) интегрируемости, можно представить в виде преобразования Фурье, или другими словами, можно разложить в спектр:

(1.11)

Вторая формула записана для одномерной функции . Параметры x и h называются пространственными частотами, а преобразование (1.11) называют разложением в спектр пространственных частот.

Существует и обратное преобразование Фурье, которое позволяет найти распределение , если известна функция спектра

(1.12)

Формулы приведены соответственно для двумерного и одномерного случаев.

Проиллюстрируем физический смысл понятия " пространственная частота " на следующем примере. Возьмем в качестве подынтегрального выражения плоскую волну, волновой вектор которой лежит в плоскости x0z.

. (1.13)

Подставив (1.13) в (1.12), получим*

(1.14)

Здесь имеет размерность пространственной частоты [см^-1],

(1.15)

а величина − это пространственный период волны в направлении оси 0 х (см. рис. 1.1). Наклонными линиями на рис.1.1 условно изображены следы плоскостей равной фазы, расположенные на расстоянии l друг от друга. Колебания в соседних плоскостях отличаются по фазе на . Отсюда видно, что величина − пространственная частота поверхностей равной фазы по направлению вдоль оси 0х. Итак, плоская волна, распространяющаяся под углом q ₁ к плоскости у0z, характеризуется пространственной частотой:

.

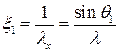Таким образом, плоская волна с пространственной частотой имеет пространственный спектр в виде -функции, расположенной на пространственной частоте на шкале пространственных частот .

Аналогично в случае, если волновой вектор плоской волны имеет компоненты k_х и k_у, то пространственный спектр волны имеет вид , где - пространственная частота по оси 0y.

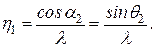
Разложение сложного волнового фронта в спектр по пространственным частотам является фактически разложением волны на элементарные плоские волны. Необходимо иметь в виду, что если в плоскости z = 0 произведено разложение сложной волны в пространственный спектр, то придвижении этой волны в свободном пространстве от исходной плоскости к другой плоскости z = , фазовые соотношения в пространственном спектре изменятс я. Изменение происходит за счет разных фазовых сдвигов плоских волн, имеющих различные пространственные частоты. Этот процесс можно описать функцией передачи свободного пространства , котораяможет быть получена из выражения (1.9), и имеет вид:

(1.16)

Таким образом, пространственный спектр в плоскости , которая находится на расстоянии 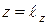от плоскости , можно выразить через пространственный спектр в плоскости , используя следующее соотношение:

(1.17)

При практических расчетах оптических схем нередко применяют приближение малых пространственных частот. Полагая, что и , можно записать:

(1.18)

Если подставить это разложение в формулу (1.16), то получим:

(1.19)

Подчеркнутый сомножитель в (1.19) в дальнейшем отбрасывают, поскольку он дает постоянный фазовый сдвиг волны, однородный по всему волновому фронту и не зависит от пространственной частоты. Эта фазовая функция не детектируется теми приборами и средствами наблюдения, с помощью которых изучают распределение интенсивности светового пучка в плоскости наблюдения. В дальнейшем при анализе одномерных задач мы будем пользоваться следующей формулой функции передачи участка свободного пространства:

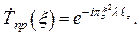(1.20)

Поиск по сайту: