О преобразовании пространственной модуляции при прохождении волны в свободном пространстве

Пусть в плоскости 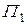расположена амплитудная решетка (см. рис. 1.15). с распределением (1.104) с глубиной модуляции .Поставим задачу: найти распределение амплитуд и фаз оптической волны в плоскости , которая расположена от плоскости 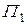на расстоянии 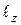вдоль оси 0z. Для сокращения записи и для упрощения анализа положим, что решетка бесконечна в направлении 0х.

. (1.104)

Рис. 1.15. К расчету распределения амплитуд в плоскости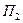

. (1.104)

Решение. После прохождения через решетку в плоскости 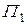распределение амплитуд волны имеет вид: . Найдем пространственный спектр волны в плоскости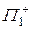

(1.105)

Далее оптическая волна распространяется от плоскости 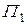до плоскости в свободном пространстве и разные компоненты пространственного спектра получают различные фазовые задержки. Чтобы найти пространственный спектр в плоскости , мы должны умножить спектр в плоскости 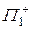на пространственно-частотную передаточную функцию участка свободного пространства .

. (1.106)

Рассмотрим эту задачу, ограничившись приближением невысоких пространственных частот. При этом воспользуемся приближенной формулой (1.20), записав:

. (1.107)

После подстановки (1.105) и (1.107) в (1.106) получим:

(1.108)

По найденному пространственному спектру в плоскости (1.108) можно рассчитать распределение амплитуд и фаз оптической волны в этой плоскости. Для этой цели используется обратное преобразование Фурье:

(1.109)

Формулу (1.109) можно записать в виде:

. (1.110)

Анализ полученного результата. Выражение (1.110) отличается от исходного выражения (1.104) дополнительным множителем перед косинусом.

Рассмотрим некоторые характерные плоскости, расположенные на расстояниях:

; ; .

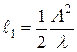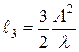Проследим, как трансформируется распределение амплитуд при переходе от одной плоскости к другой.

При имеем: = .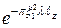

Для этого случая из (1.110) получим следующее распределение амплитуд в плоскости :

. (1.111)

Выражение (1.111) описывает уже не амплитудную, а фазовую модуляцию. В самом деле, функция фазовой модуляции при малой глубине модуляции может быть представлена как

,

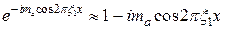что совпадает с выражением (1.111).

При имеем : распределение амплитуд имеет вид:

. (1.112)

Выражение (1.112) описывает амплитудную пространственную модуляцию, однако по сравнению с исходной модуляцией в плоскости она находится в противофазе.

Анализируя дальнейшее движение плоскости наблюдения вдоль оси z, можно убедиться, что при дистанции 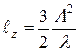модуляция вновь станет фазовой, а при функция модуляции превратится в исходную функцию (1.104). При дальнейшем движении по z картина будет повторяться. Следует помнить, что все эти выводы получены в предположении, что размеры решетки бесконечны. При конечном размере решетки в направлении оси 0х в дифракционной картине будут наблюдаться искажения: вначале на краях апертуры, а с удалением плоскости наблюдения эти искажения будут все более заметны по всей апертуре решетки. Точный расчет распределений амплитуд и фаз ограниченной решетки можно провести лишь с применением численных методов. Вместе с тем можно заведомо указать область, где модель бесконечных решеток совершенно неприменима: это область, где т.е. . В этой области пучки +1 и -1 порядков дифракции разделяются в пространстве и более не будут участвовать в интерференции. Результаты данного анализа могут дать удовлетворительное совпадение с экспериментом при . Например, при D = 10 мм, L = 0,1 мм, l = 0,63 мкм, получим ~ 790 мм,

Поиск по сайту: