Преобразование Фурье в оптической схеме с линзой

Рассмотрим оптическую схему, изображенную на рис.3.4. Плоский транспарант расположен в плоскости P₁. Пусть - комплексная функция пропускания транспаранта. В этой же плоскости расположена тонкая собирающая оптическая линза с фокусным расстоянием, равным f _л. Систему, состоящую из транспаранта и линзы, просвечивают слева в направлении оси 0z плоской оптической волной с амплитудой а ₀.

Рис.3.4. Схе ма расположения транспаранта и линзы.

Плоскость наблюдения оптической волны расположена справа от линзы на расстоянии, равном фокусному расстоянию линзы . Рассмотрим процесс преобразования волны при ее распространении от плоскости 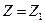до плоскости . Выразим распределение комплексной амплитуды волны непосредственно за плоскостью P₁ (в плоскости, которую обозначим ), после прохождения плоской волны через транспарант и линзу. Для этого помножим функцию распределения волны на входе системы на функцию передачи транспаранта и на функцию пропускания тонкой линзы:

(3.28)

Далее волна распространяется в свободном пространстве до плоскости наблюдения, которая находится на расстоянии . Для расчета поля в плоскости P₂ при заданном распределении амплитуд в плоскости можно воспользоваться формулой дифракционного интеграла при малых углах дифракции, т.е. в параксиальном приближении.

Распределение тогда можно выразить:

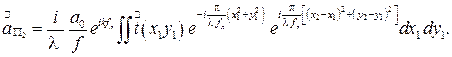(3.29)

Интегрирование в формуле (3.29) проводится по апертуре. Однако, учитывая, что за пределами рассматриваемой апертуры поле равно нулю (можно установить непрозрачный экран, окружающий апертуру), можно расширить пределы интегрирования от -µ до +µ.

Кроме того, преобразуем подынтегральное выражение, раскрыв квадраты разностей: и . После подстановки этих выражений в формулу (3.29) получим:

(3.30)

Введем некоторые обозначения:

. (3.31)

Углы q₁ и q₂ – между направлением на соответствующие точки с координатами х ₂ и у ₂ и осью 0z. Соотношения записаны в приближении малых углов q.

Заменив и , мы получим:

(3.32)

Как видно формы выражений величин x и h совпадают с формой выражений для пространственных частот, которые мы рассматривали выше, в разделе 1. С учетом (3.32) выражение (3.30) принимает следующий вид:

(3.33)

Подчеркнутая часть выражения (3.33) является интегралом Фурье. Множитель перед интегралом состоит из постоянного сомножителя, не зависящего от и фазового множителя , отражающего кривизну волнового фронта в плоскости . Если рассматривать распределение интенсивности в плоскости P₂(), то учитывая, что , все мнимые сомножители перед интегралом при умножении на комплексно сопряженные превратятся в единицы. Распределение плотности мощности в фокусе линзы с точностью до постоянного множителя будет равно квадрату модуля функции преобразования Фурье от распределения амплитуд в плоскости P_{1 ,} а в другой терминологии спектру мощности функции .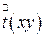

Поиск по сайту: