Задач нахождения пространственного спектра

Сверткой двух функций и называют функцию, которая определяется следующим интегральным преобразованием:

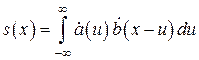. (1.40)

В подынтегральное выражение функции свертки одна из функций входит в обращенном виде, .

Функция свертки обозначается сокращенно .

Функцию корреляции двух функций мы будем обозначать символом . Эта функция отличается от функции свертки, и определяется так:

. (1.41)

Отдельные точки функций свертки и корреляции вычисляются как интегралы при различных значениях сдвига x одной из функций относительно другой. Для вычисления свертки функций сложной формы необходимо применять численное интегрирование. Для некоторых простейших функций вычисления сводятся к табличным интегралам. Рассмотрим один из таких примеров.

1.7.1. Свертка двух прямоугольных импульсов с единичной амплитудой и с протяженностью каждого из них от до . Графики исходных функций изображены на рис. 1.9. Эти функции могут быть выражены следующим соотношением:

(1.42)

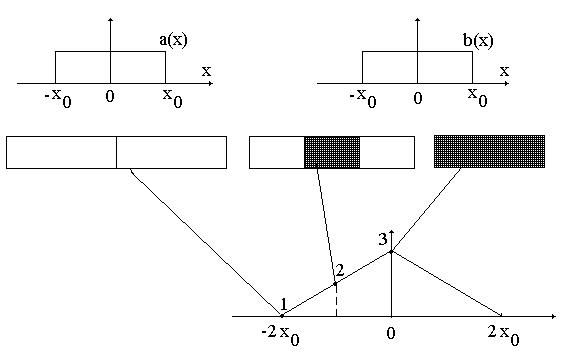Рис.1.9. Иллюстрация формирования свертки двух функций прямоугольной формы. Вверху показана форма исходных функций. Внизу показана форма функции свертки. Посредине показано перекрытие функций, соответствующее различным точкам функции свертки.

При вычислении интеграла свертки функций (1.42) разобьем его на два интеграла: один для сдвигов 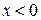, другой для сдвигов 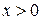. Первый интеграл (для х < 0) отличен от нуля при величинах сдвига x в пределах от –2 х ₀ до x=0.

При этом в результате интегрирования получим линейно возрастающую функцию на интервале (–2 х _0, 0):

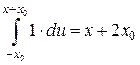. (1.43)

Аналогично, второй интеграл не равен нулю при сдвигах от х=0 до x= . При этом в результате интегрирования получим линейно убывающую функцию на интервале (0, 2 х ₀):

(1.44).

График функции свертки, построенный по формулам (1.43) и (1.44) и представленный на рис. 1.9, − это треугольник с протяженностью от координаты до . Для наглядности на рис. 1.9, приведены графические иллюстрации образования интеграла свертки. Величина интеграла свертки в заданной точке определяется площадью заштрихованной фигуры, полученной в результате перемножения двух исходных функций при заданном сдвиге функции .

Свертка с d -функцией. Пусть одна из функций является d -функцией, например, . Тогда интеграл свертки дает следующий результат:

. (1.45)

Таким образом, свертка функции с d -функцией дает результат в виде исходной функции , смещенной по координате х на величину смещения d -функции .

1.7.2. Фурье-преобразование свертки двух функций. Рассмотрим фундаментальное соотношение, которое связывает функции , и их Фурье преобразования , .

Пусть функция имеет Фурье-преобразование :

. (1.46)

Пусть функция имеет Фурье-преобразование :

. (1.47)

Преобразование Фурье определено соотношением (1.11). Существует и соответствующее обратное преобразование, определяемое соотношением (1.12).

Пусть свертка двух функций имеет Фурье-преобразование

. (1.48)

Поставим задачу: выразить функцию спектра через известные нам спектры исходных функций, входящих в свертку, т.е. через функции и .

Теорема о Фурье-образе свертки формулируется следующим образом: Фурье-образ свертки двух функций равен произведению Фурье образов функций, входящих в свертку.

× . (1.49)

Это соотношение можно получить, выполнив следующие преобразования. Исходя из выражения для свертки, заменим одну из функций ее обратным Фурье преобразованием и затем изменим порядок интегрирования:

(1.50)

Последний интеграл в круглых скобках − это не что иное как Фурье-образ функции , т.е. . В итоге уравнение (1.50) можно переписать в виде:

(1.51)

Это уравнение по форме совпадает с обратным преобразованием спектра в функцию :

Отсюда следует, что

, (1.52)

что и требовалось доказать: спектр свертки двух функций равен произведению спектров функций, образующих свертку.

Существует аналогичная обратная теорема: если имеется функция , равная произведению двух функций:

, (1.53)

то спектр ее равен свертке спектров этих функций:

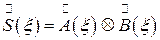. (1.54)

Эту теорему можно кратко записать в следующем виде:

. (1.55)

Применение теоремы о свертке может существенно упростить процедуру анализа оптических систем. Рассмотрим, как можно применить теорему о свертке к решению предшествующей задачи о дифракции когерентной оптической волны на амплитудной дифракционной решетке.

1.7.3. Пространственный спектр дифракционной решетки с ограниченными размерами. Имеется амплитудная дифракционная решетка с размером D вдоль оси х. Функция пропускания решетки описывается выражением (1.24). Найти пространственный спектр волны после прохождения решетки. Падающая волна − плоская с амплитудой .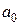

Используем следующий подход к задаче. Функцию пропускания решетки представим в виде произведения функции пропускания двух объектов:

а) бесконечной дифракционной решетки с функцией пропускания

, (1.56)

где обозначено ,

б) окна в виде щели с размером D с функцией пропускания

(1.57)

Поскольку функция пропускания системы равна произведению функции пропускания решетки на функцию окна,

, (1.58)

то, пользуясь теоремой о свертке, можно выразить пространственный спектр функции через свертку функций , которые являются соответствующими Фурье преобразованиями от функций , , т.е.

, где (1.59)

, (1.60)

. (1.61)

Спектр бесконечной решетки* с функцией пропускания (1.56) выражается через сумму d -функций

(1.62)

Здесь использовано соотношение

(1.63)

По существу спектр (1.6.2) - это спектр дифрагированных волн на выходе оптической схемы, содержащей дифракционную решетку (1.56) при облучении ее плоской волной с единичной амплитудой и направленной вдоль оси 0z.

Спектр функции − это спектр щели в непрозрачном экране. Он был рассмотрен в задаче 1.4.1 и определяется формулой (1.22) при 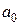= 1:

.

Из этих двух спектров легко сконструировать результирующий пространственный спектр на выходе дифракционной решетки ограниченных размеров при освещении ее плоской волной с амплитудой 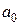, направленной вдоль оси 0z.

(1.64)

В результате мы получили выражение, тождественное ранее полученному выражению (1.27). Привлекательность данной методики расчета заключается в ее универсальности и простоте. На этом примере видно, что если форма функции окна изменится, это скажется только на форме линий спектра, а расположение линий не изменяется. Так, если Фурье-образ окна будет не , а каким-либо другим, , то в последнем выражении вместо функции должна быть записана функция и смещенные функции .

Поиск по сайту: