Пространственный спектр фазовой решетки при малой глубине модуляции

Поставим задачу: Найти пространственный спектр фазовой гармонической решетки при малой глубине фазовой модуляции, когда .

Решение этой задачи можно получить как частный случай решения предыдущей задачи, из формулы (1.82). Как известно, см. [1], стр. 519, функция Бесселя для целых положительных индексов п может быть представлена в виде:

, (1.83)

т.е.

, (1.84)

, (1.85)

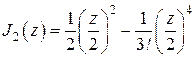. (1.86)

Функцию Бесселя с целыми отрицательными индексами можно выразить через функции Бесселя с положительным индексом:

. (1.87)

При малых значениях аргумента можно отбросить все члены, содержащие z в степени выше первой. При этом сохраняется только три ненулевые функции:

,

,
.

В результате пространственный спектр дифракции на фазовой гармонической решетке с малой глубиной будет иметь вид:

. (1.88)

Здесь имеются лишь три компоненты спектра: на нулевой пространственной частоте и на пространственных частотах и . По составу пространственных частот этот спектр похож на спектр амплитудной гармонической решетки, однако он отличается от спектра амплитудной решетки фазовыми соотношениями между составляющими спектра.

Поиск по сайту: