Некоторые типы фазовых решеток и их характеристики

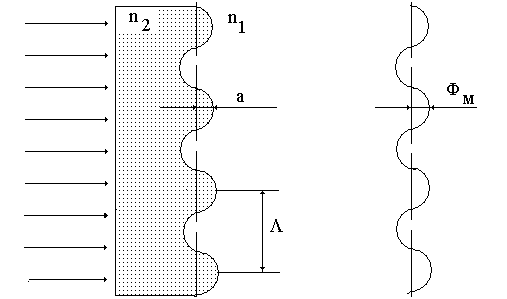
Рис.1.10. Фазовая решетка с гармоническим профилем, образованная

рельефом на поверхности. Справа изображена функция модуляции

вол нового фронта.

Рис. 1.11. Фазовая решетка с прямоугольным профилем, образованная рельефом на поверхности. Справа изображена функция модуляции

вол нового фронта.

Решетки, образованные рельефом на поверхности прозрачного тела, изображены на рис. 1.10, и рис 1.11. При прохождении через прозрачную пластинку с рельефом, расположенным на поверхности, оптическая волна получает пространственную фазовую модуляцию (ПФМ) волнового фронта. Форма ПФМ зависит от формы рельефа, а амплитуда пространственной фазовой модуляции зависит от глубины рельефа и показателя преломления.

Функция пропускания фазовой решетки описывается выражением

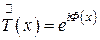, (1.65)

где 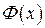− функция формы фазовой модуляции.

Для гармонической фазовой решетки, изображенной на рис. 1.10, функцию можно выразить формулой:

, (1.66)

где 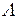− период решетки; х ₀ − сдвиг относительно начала координат. Для решетки с прямоугольным профилем, изображенным на рис. 1.11, функция формы имеет вид:

(1.67)

где k = 0, 1, 2, ¼

Величина − амплитуда пространственной фазовой модуляции, она может быть рассчитана как половина разности фаз оптических лучей, проходящих через точки максимальной и минимальной высоты рельефа (луч 1 и луч 2 на рис. 1.11). Таким образом, для рельефных решеток получаем следующие соотношения:

(1.68)

(1.69)

(1.70)

(1.71)

где − показатели преломления сред по разные стороны границы рельефа, в частности, если рельеф граничит с воздухом, то можно считать , - глубина рельефа, - амплитуда рельефа.

Решетка, образованная за счет изменения показателя преломления материала. Для решетки, образованной изменением показателя преломления прозрачной пластины на ее различных участках, получаем следующее соотношение, определяющее амплитуду фазовой пространственной модуляции волны после ее прохождения через решетку по нормалям к поверхности

(1.72)

Формула (1.72) справедлива только для нормального падения оптического луча на решетку.

Отражающие фазовые решетки (рис. 1.12 и 1.13). Поставим задачу: Найти глубину пространственной фазовой модуляции, которую получит световая волна в случае отражения от поверхности с периодическим рельефом. Положим, что на поверхности имеется периодический рельеф с периодом 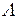и с глубиной рельефа h. Положим, что коэффициент отражения оптической волны одинаков на всех участках поверхности (на выступах и впадинах). Отражаясь от такой поверхности с периодическим рельефом, световая волна получает периодическую пространственную фазовую модуляцию.

Рассмотрим вначале случай нормального падения. Выразим оптические пути лучей А и В (см. рис. 1.12) через длину оптической волны l и глубину рельефа h (или его амплитуду а). В плоскости z = 0 фазовый набег луча А равен скачку фазы при отражении ; фазовый набег луча В равен сумме скачка и удвоенного фазового набега на длине h, равной глубине канавки

Рис.1.12.К расчету оптической разности хода лучей А и Б при нормальном падении волны на отражающую решетку.

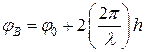. (1.73)

Разность фаз лучей В и А равна:

. (1.74)

Амплитуда ПФМ, полученная в результате отражения, будет:

(1.75)

Случай наклонного падения (рис. 1.13 ). Рассматривая лучи А и В, распространяющиеся в воздухе, один из которых отражается от выступа в точке L, а второй от дна впадины в точке К, построим линии волновых фронтов падающей и отраженной волн LM и LN, перпендикулярные к лучам А и В. Оптическая разность хода будет определяться суммой фазовых набегов на отрезках МК и KN

, (1.76)

. (1.77)

В результате при наклонном падении мы получаем пространственную фазовую модуляцию с глубиной, меньшей, чем при нормальном падении. На этот, с первого взгляда, неожиданный результат следует обратить внимание.

Рис.1.13. К расчету оптической разности хода лучей А и Б при наклонном падении волны на отражающую решетку.

1.8.2. Расчет пространственного спектра гармонической фазовой решетки. Рассмотрим вначале гармоническую фазовую решетку, имеющую бесконечные размеры. Пусть функция пропускания решетки описывается следующей формулой:

, (1.78)

где , а 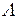− период решетки.

Разложим периодическую функцию пропускания в ряд Фурье. В курсе высшей математики В.И. Смирнова [17] т. III, стр. 530 можно найти следующую формулу разложения:

. (1.79)

Здесь 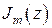− функции Бесселя 1 рода с целыми индексами т = 0, ±1, ±2, ¼

Применив эту формулу к функции (1.78), получим следующее выражение:

. (1.80)

Оптическая волна на выходе при освещении решетки плоской волной будет иметь вид 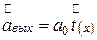. Используя разложение в ряд (1.80), легко рассчитать пространственный спектр волны по формуле (1.11). Подставив (1.80) в формулу (1.11), получим:

. (1.81)

Используя методику, изложенную выше (в разделе 1.6.3 при анализе амплитудной решетки), нетрудно перейти от неограниченной решетки к решетке конечных размеров. Для этого в плоскости решетки поместим "окно", то есть апертуру конечного размера.. Если, например, окно имеет форму щели и его пространственный спектр описывается функцией (1.22); т.е. , то и спектр решетки будет содержать не ряд d -функций, как (1.81), а ряд функций , т.е.

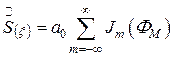
. (1.82)

Соотношение амплитуд дифракционных волн в дифракционных порядках описывается, как видно, функциями Бесселя. Информацию о свойствах функций Бесселя можно найти в справочниках, например, в [19] на стр. 192, 193, Графики зависимостей приведены в справочнике [20], с. 390, а также в курсе высшей математики Смирнова, т. III [17].

При экспериментах измеряют интенсивности дифракционных порядков, поэтому целесообразно рассмотреть соотношения интенсивностей излучения в дифракционной картине. Если дифракционная решетка − фазовая с гармоническим профилем, с амплитудой ПФМ, равной , то величины интенсивностей излучения, дифрагированного в различные порядки, выражается через квадраты соответствующих функций Бесселя: , . Соотношения между интенсивностями разных порядков дифракции выражаются через соответствующие отношения квадратов функций Бесселя. Так, например, отношение интенсивности дифрагированного пучка первого порядка к интенсивности нулевого порядка можно выразить так: .

Максимум первой функции Бесселя, а следовательно и наибольшее значение мощности дифрагированного пучка в первых порядках будет наблюдаться при = 1,84, при этом = 0,5819. Эффективность дифракции на фазовой решетке с гармоническим профилем в первом порядке дифракции, т.е. отношение мощности излучения, дифрагированного в первый порядок к мощности излучения на входе, составит = 0,339 = 33,9%. Сравнивая эту величину с эффективностью дифракции на амплитудной гармонической решетке можно отметить значительно более высокую эффективность дифракции на фазовой дифракционной решетке.

Следует заметить, что модель гармонической фазовой решетки оказывается весьма полезной для описания дифракционных явлений при взаимодействии света с ультразвуковыми волнами, распространяющимися в прозрачных средах. Эти явления рассматриваются в разделах, посвященных акустооптике.

Поиск по сайту: