Соотношение между мощностью падающего на апертуру и мощностью дифрагированного излучения при дифракции света на щели

Между мощностью световой волны, выходящей из излучающей апертуры, и мощностью, заключенной во всех компонентах пространственного спектра, существует связь, описываемая равенством Парсеваля, см. [4, 8]:

(1.30)

Здесь − распределение амплитуды волны по апертуре, а − распределение амплитуд элементарных плоских волн в пространственном спектре.

Выражение (1.30) отражает закон сохранения энергии. Мощность, излученная с апертуры, полностью расходуется на создание волн пространственного спектра и равна суммарной мощности всех его компонент.

Рассмотрим, как выполняется соотношение (1.30) при дифракции плоской волны на щели. Мощность волны, прошедшей через апертуру размером 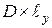можно рассчитать, вычислив интеграл в левой части равенства (1.30):

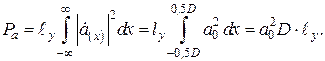(1.31)

Интеграл по пространственным частотам в правой части равенства (1.30) выражает мощность излучения на всех пространственных частотах пространственного спектра. Форма пространственного спектра при дифракции света на щели была найдена ранее (см. формулу 1.22). Подставив (1.22) в интеграл получим:

(1.32)

Из сопоставления выражений (1.31) и (1.32) видно, что соотношение Парсеваля выполняется. При вычислении интеграла (1.32) использовано следующее соотношение, взятое из справочника [18], стр. 192, интеграл 858.652.

. При п = 1 и в пределах получим .

Поиск по сайту: