Волна вероятности

Предыдущая глава закончилась констатацией, что мы пока не установили, что именно колеблется при движении электрона. В истории физики такое уже случалось. Когда-то при выводе уравнений электродинамики Максвелл тоже не знал, что представляют собой описываемые им колебания и волны, но уравнения оказались верны. Поэтому отложим пока вопрос о физической природе волн де Бройля и просто введем некую «электронную» волну, то есть волновую функцию Y(t, r). О ней мы знаем пока только одно: волновая функция должна описывать результаты опытов, доказывающих волновые свойства электронов (дифракцию и т. п.).
Представим мысленно эксперимент В.А. Фабриканта (см. разд.3.2. Волны материи), в котором электроны поочередно направлялись на кристалл, играющий роль дифракционной решетки. За кристаллом помещалась фотопластинка, на которой в конце концов возникали типичные дифракционные кольца. Из классической физики известно, какие математические средства описывают такую картину: обычное сложение интерферирующих волн, интенсивности которых пропорциональны

Правда, в отличие от обычной волны электрон не делится на части: при прохождении электронов через кристалл каждый из них попадает в какую-то одну точку на фотопластинке, вызывая почернение именно здесь и нигде больше. В этом проявляются свойства электрона как частицы. Несмотря на одинаковые начальные условия, электроны, как показал опыт, попадают в разные точки. О данном конкретном электроне заранее неизвестно, в какую именно точку на пластинке он попадет. В этом проявляются его волновые свойства. Дифракционная картина возникает, когда через кристалл пройдет достаточно много таких электронов. Интенсивность почернения пластинки в данной точке пропорциональна числу попавших туда частиц, то есть вероятности попадания.
В классической же физике почернение пластинки определяется интенсивностью волны, то есть квадратом модуля волновой функции. Выходит, что величина

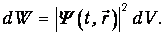
(4.1)

Иными словами

- это плотность вероятности найти частицу в точке с координатой r.

Вероятность W(V) найти частицу в каком-то конечном объеме V вычисляется с помощью сложения вероятностей, то есть интегрированием

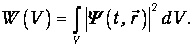
(4.2)

Интегрирование в (4.2) ведется по объему V (в случае одномерного движения - по отрезку).

Полная вероятность найти частицу хоть где-нибудь в пространстве должна быть равна единице. Отсюда - так называемое условие нормировки волновой функции: такой же интеграл по всему пространству равен единице, то есть

(4.3)

Замечание: выполнение этого условия возможно для тех задач, в которых классическая частица движется в ограниченной области пространства (финитное движение). Для других движений условие нормировки усложняется.

Наблюдаемые физические величины должны описываться действительными числами и функциями. Соответственно, мы представляли классические волны (звуковые, электромагнитные) в виде

Можно было бы воспользоваться математическим формализмом комплексных чисел, основываясь на формуле Эйлера

где
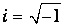- мнимая единица. Тогда ту же волну можно было бы представить в виде действительной части выражения

(4.4)

Где

Начальная фаза здесь включена в комплексную амплитуду А. В применении к классическим волнам оба формализма эквивалентны, так как в конечном итоге берется только действительная часть волны. В отличие от классических волн, волна вероятности комплексна. Физические наблюдаемые величины выражаются через квадрат модуля волновой функции, так что и в квантовой механике они будут описываться действительными числами. Но комплексность волновой функции имеет глубокую связь с законом сохранения электрического заряда, так что применение комплексных чисел и функций в квантовой механике - не прихоть, а необходимость. Поверхность постоянной фазы в волне X (4.4) распространяется вдоль волнового вектора k, фазовая скорость волны по-прежнему равна

так что переход к комплексным волнам не меняет привычных нам соотношений.

Поиск по сайту: