 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Ступенчатый потенциал
Этот потенциал мы снова изобразим на рис.4.5.
Рис. 4.5. Прохождение частицы над ступенчатым барьером: процесс эквивалентен нормальному падению света из вакуума (/) на полубесконечную среду (2) с показателем преломления
Установление аналогии между квантовой механикой и светом означает, что мы хотим найти такие замены квантово-механических характеристик движения частицы на характеристики света, чтобы формулы квантовой механики перешли в соответствующие формулы для распространения света. Процедура замены будет изображена в формулах двойными стрелками, причем слева будут стоять квантово-механические величины, а справа - оптические. От этих формул следует отличать равенства, где по обе стороны стоят величины, относящиеся либо к частице, либо к световой волне.
Распространение квантовой частицы описывается в терминах ее волнового вектора
где
- кинетическая энергия частицы. Здесь и далее мы выписываем для частицы формулы, относящиеся к области барьера; соотношения для частицы вне барьера получаются при U=0. Скорость частицы дается соотношением
| (4.36) |
Введем прежде всего показатель преломления п среды 2, соответствующий области барьера: его естественно определить, как отношение скоростей частицы в областях 1 и 2 (считаем, что в области 1 показатель преломления равен единице, как в вакууме, то есть n21=n)
| (4.37) |
При U=0 получаем п=1 - показатель преломления вакуума.
Волновой вектор световой волны связан с круговой частотой соотношением
Мы предположим также, что волновой вектор частицы перейдет при искомой замене в волновой вектор света, то есть
| (4.38) |
Из соотношения
для среды без дисперсии следует групповая скорость света
в которую при искомой замене должна перейти скорость частицы v. Тогда уравнение (4.36) дает
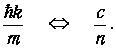
| (4.39) |
Разделив уравнение (4.38) на (4.39), находим еще одну замену
| (4.40) |
Конечно, «массу», стоящую здесь в левой части, нельзя отождествлять с массой фотона, которая равна нулю. Можно назвать ее «эффективной массой фотона». В вакууме, при п=1, она равна
Эта величина соответствует известной релятивистской связи масса - энергия, и она возникает при изучении влияния гравитационного поля на распространение световых лучей.
Как бы то ни было, но суть в том, что указанные замены, как мы увидим, переводят формулы квантовой механики в формулы оптики.
Рассматривая прохождение частицы над низким потенциальным барьером (см. ступенчатый потенциал на рис. 4.5), мы уже вывели коэффициент прохождения, который здесь обозначим Ds:
| (4.41) |
Коэффициент отражения (30.32), равный Rs=1-Ds, переписываем в виде
| (4.42) |
Применяя вышеуказанные замены, сводящиеся в данном случае к замене
мы записываем соответствующие коэффициенты прохождения и отражения для света, падающего перпендикулярно из вакуума на среду с показателем преломления п:
| (4.43) |
В оптике точно такие формулы называются формулами Френеля для относительной интенсивности отраженного и преломленного света при угле падения 90°. Мы еще раз убедились, что физика (или природа) - едина, и квантовая механика имеет глубокие корни не только в классической механике, но и в волновой оптике.
Поиск по сайту: