Частица в бесконечно глубокой потенциальной яме

Потенциальная энергия в этой задаче имеет вид

(4.23)

Такая система соответствует частице, движущейся вдоль прямой линии и отскакивающей от абсолютно отражающих препятствий в точках х=0 и х=l. В область бесконечного потенциала частица проникнуть не может, следовательно, y(х)=0 за пределами отрезка [ 0, l ]. Внутри ямы U(x)=0, и стационарное уравнение Шредингера имеет тот же вид, как для свободной частицы. Получатся те же решения в виде суперпозиции стоячих (или бегущих) волн, но в отличие от предыдущего случая добавятся граничные условия. Именно, в точках х=0 и х=l волновая функция должна обращаться в нуль (поскольку она непрерывна и равна нулю вне ямы). В классической механике точно такие граничные условия имеет уравнение для закрепленной струны.

Общее решение имеет вид

Используем сначала первое граничное условие

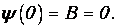
Мы получили, что решение уравнения Шредингера должно иметь вид

Если продолжить нашу аналогию, то можно сказать, что на струне, закрепленной в одной точке, бегущих волн не бывает: отражение от неподвижной точки обязательно порождает стоячую волну. Однако на длину волны никаких ограничений не накладывается: такая струна также не звучит.

Теперь наложим второе из граничных условий:

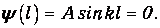
Здесь есть два типа решений. При А=0 получаем

что означает отсутствие частицы в яме (вероятность найти ее всюду равна нулю). Поэтому нас интересует второе решение, когда

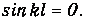
Это возможно лишь при некоторых значениях волнового вектора:

Так как энергия частицы связана с волновым вектором, то

(4.24)

Мы получили квантование энергии, то есть наша «струна», закрепленная с обеих сторон, зазвучала, так как появились выделенные частоты.

Подставляя найденные разрешенные значения волнового вектора в выражение для волновой функции, получаем ее в виде

(4.25)

Смысл квантового числа п: оно на единицу больше числа нулей волновой функции. Значение постоянной

определяется из условия нормировки.

Откуда же берется дискретность уровней энергии, характерная и для атома? Сравним со свободной частицей: уравнения те же, но с иными граничными условиями! Здесь возможны две постановки задачи. В первом случае исследуется состояние, которому в классической механике соответствовало бы инфинитное движение (задача рассеяния). Обычно в таких случаях решения возможны при любых значениях энергии Е (как говорят, спектр непрерывен). Во втором случае исследуется состояние, которому в классике соответствует финитное движение в ограниченной области пространства (задача на связанные состояния). Требование конечности волновой функции во всем пространстве ведет к квантованию энергии. Подчеркнем: в этом случае стационарное уравнение имеет физически приемлемые решения не всегда, а лишь при некоторых значениях Е. Как следствие возникает дискретный спектр энергии системы.

Пример. Определим разность соседних уровней энергии DЕ для частицы в бесконечно глубокой потенциальной яме при больших значениях п. Полученный результат используем для оценки разности энергий соседних уровней молекул азота при комнатной температуре Т=300 К в сосуде. Примем массу молекулы m=2.3 · 10^-26 кг, а линейный размер сосуда l=0.1 м. Сравним полученный результат с кинетической энергией поступательного движения молекул азота.

Используя выражение (4.24) для уровней энергии частицы в потенциальной яме, находим разность энергий соседних уровней

при больших значениях п. Средняя кинетическая энергия поступательного движения молекул азота равна

Приравнивая Е выражению (4.24) для энергии уровней частицы в яме, находим, что такая энергия соответствует квантовым числам порядка

Уже само по себе это число говорит о том, что в области крайне высоких возбуждений работают классические формулы. Разность энергий соседних уровней получаем, подставляя в формулу для DЕ найденное выражение для квантового числа п:

В электрон-вольтах те же характеристики имеют значения

Относительная разность энергий соседних уровней ничтожно мала:

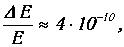
и потому в классическом пределе квантовой дискретностью пренебрегают.

Поиск по сайту: