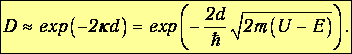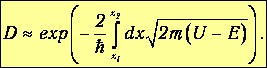Потенциальный барьер конечной ширины

Потенциальная энергия имеет вид

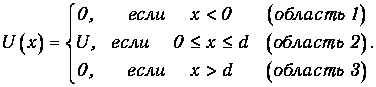
(4.33)

Ясно, что происходит при Е>U: с некой вероятностью частица может отразиться от барьера. Наиболее интересен случай Е<U (рис. 4.3).

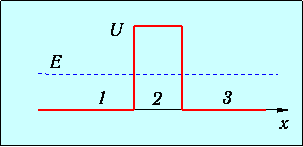
Рис. 4.3. Потенциальный барьер конечной ширины

Мы видели, что интенсивность (квадрат модуля амплитуды) волны убывает под барьером и на расстоянии d становится меньше в exp(-2dk) раз. Но в этой точке барьер кончается, так что волна выйдет на свободу с уменьшенной амплитудой.

Отношение интенсивностей выходящей и падающей волн называется коэффициентом прозрачности D (он же равен вероятности прохождения через барьер). Из наших рассуждений следует приближенное выражение для него

(4.34)

Получая D, мы опустили некие множители перед экспонентой, что по физическому смыслу означает пренебрежение процессами, когда частица, прежде чем выйти из-под барьера, испытает многократное отражение от его стенок. При высоком и широком барьере (D<<1) вклад таких процессов невелик и сделанное приближение оправдано.

Проникновение частицы сквозь конечный потенциальный барьер возможно в квантовой механике, но категорически запрещено в классической. В самом деле, формально величина hk играет роль импульса (мнимого), так что кинетическая энергия

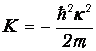
становится отрицательной. Дело спасают соотношения неопределенностей. Модуль (мнимой) скорости частицы имеет порядок

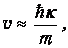
так что время туннелирования

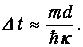
Неопределенность в кинетической энергии

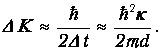
Из полученных результатов для коэффициента прозрачности видно, что эффект туннелирования заметен, если

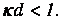
Но тогда

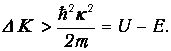
Получается, что неопределенность в кинетической энергии частицы под барьером больше самого значения кинетической энергии. Поэтому нельзя утверждать, что под барьером кинетическая энергия отрицательна. Скорее, она «размыта» настолько, что частица может как бы перепрыгнуть не слишком большой барьер. В случае же высокого и широкого барьера «размытость» кинетической энергии должна быть очень велика, что возможно лишь на очень короткое время, за которое частица не успевает проскочить за барьер. Поэтому в этом случае коэффициент прозрачности становится экспоненциально малым. По-другому: туннелирование заметно при ширине барьера порядка длины волны де Бройля.

Барьер произвольной формы можно представить в виде последовательности прямоугольных барьеров; теорема об умножении вероятностей ведет к появлению суммы (интеграла) в экспоненте, так что вместо (4.34) имеем

(4.35)

Интеграл берется между точками поворота

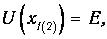
в которых классическая частица должна изменить направление движения.

Пример 1. Электрон находится в одномерной потенциальной яме шириной а=10^{-10 м} (рис. 4.4) и имеет энергию Е=1.5 эВ. С одной стороны ямы потенциальная энергия U(x) бесконечна, а с другой стороны выйти из ямы электрону мешает потенциальный барьер высотой U=2 эВ и шириной d=3 · 10^-10 м. Оценим время жизни t электрона в яме.

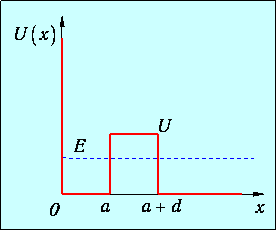
Рис. 4.4. Частица в потенциальной яме, образованной непроницаемым препятствием и конечным барьером

Скорость электрона в яме

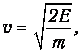
и за промежуток времени t он подойдет к барьеру

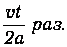
При каждом подходе вероятность туннелирования равна D, так что вероятность туннелирования W_t за время t равна

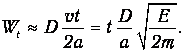
Вероятность W_t увеличивается с ростом промежутка времени t. При некотором значении t=t вероятность туннелирования станет равной единице, и электрон вырвется из ямы. Отсюда получаем для времени жизни электрона в яме оценку:

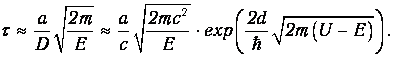
Теперь остается подставить численные данные. Для упрощения вычислений имеет смысл отдельно рассчитать коэффициент прозрачности и предэкспоненциальный множитель. Имеем

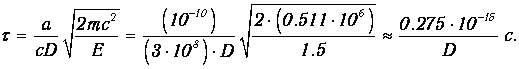
Теперь осталось рассчитать коэффициент прозрачности:

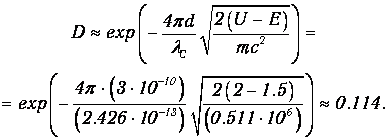
Получаем окончательно

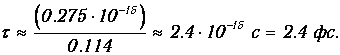
Даже по масштабам микромира это время мало: прежде чем электрон просочится сквозь барьер, свет успеет пройти расстояние всего лишь в 0.7 мкм.

Прозрачность барьера сильно зависит от энергии частицы в яме и от ширины и высоты барьера. Например, при увеличении ширины барьера в два раза новый коэффициент прозрачности будет равен, как легко догадаться, квадрату старого. Для электрона тогда получится значение D=0.0013 и его время жизни в яме увеличится до t=21 фс. Это и объясняет отсутствие туннелирования в обычном мире с его высокими и широкими потенциальными барьерами.

Пример 2. Решим предыдущий пример, поместив вместо электрона в ту же потенциальную яму протон.

Чтобы не решать аналогичную задачу с самого начала, можно воспользоваться результатами предыдущего примера. Протон массивнее электрона в п=1 836 раз. В коэффициент прозрачности масса частицы входит под квадратным корнем в показателе экспоненты. При изменении массы в п раз в показателе экспоненты появится множитель

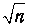
и новый коэффициент прозрачности будет равен старому, возведенному в степень

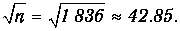
Используя данные предыдущего примера, получаем

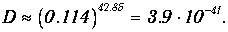
Предэкспоненциальный множительтакже умножится на

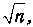
и время жизни протона в потенциальной яме будет равно

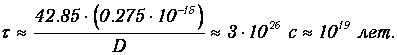
Получилась столь огромная величина, что протон будет жить в яме вечно: время существования Вселенной «всего» 15 млрд. лет.

Эти две задачи демонстрируют сильную зависимость проницаемости барьера от массы частицы.

Поиск по сайту: