 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Схема нижних уровней атома водорода
| n=1 | l=0 | j=1/2 | 1s1/2 |
| n=2 | l=0 | j=1/2 | 2s1/2 |
| l=1 | j=1/2 | 2p1/2 | |
| j=3/2 | 2p3/2 | ||
| n=3 | l=0 | j=1/2 | 3s1/2 |
| l=1 | j=1/2 | 3p1/2 | |
| j=3/2 | 3p3/2 | ||
| l=2 | j=3/2 | 3d3/2 | |
| j=5/2 | 3d5/2 |
Энергия уровней уже выражается не формулой Бора, но содержит поправки порядка величины a2. Мы не станем приводить эту формулу, но отметим ее характерное свойство: в отсутствие внешних полей энергия по-прежнему не зависит от орбитального момента (квантового числа l), но лишь от полного момента импульса (квантового числа j). Значит, уровни 2s1/2 и 2р1/2 вырождены (их энергии совпадают). Уровень 2р3/2, как оказывается, лежит чуть выше.
Состояния многоэлектронных атомов классифицируются подобным образом. Если L - суммарный орбитальный момент всех электронов, а S - их суммарный спиновый момент, то полный момент системы определяется как

Соответственно и обозначается это состояние как 2S+1XJ. Под X понимается тот же буквенный (спектроскопический) символ, обозначающий значение орбитального момента количества движения (только в этом случае используется заглавная буква). Верхний левый индекс равен числу спиновых состояний (для одиночного электрона в нем не было необходимости, так как его спин всегда равен 1/2).
Итак, пусть дано состояние 2S+1XJ. Возникает вопрос: чему равен магнитный момент системы m J? Ясно, что он направлен вдоль полного момента количества движения J, а его размерность определяется магнетоном Бора mB. Тогда

| (5.18) |
Для гиромагнитного отношения (обобщение аналогичной величины, связанной с орбитальным и спиновым моментами) можно тогда написать выражение вида

Коэффициент пропорциональности g называется множителем Ланде или просто g -фактором. Для орбитального движения g=1, для спинового магнитного момента g=2. Задача о магнитном моменте атома сводится к нахождению зависимости g от квантовых чисел J, L, S.
Ответ можно получить с помощью простой полуклассической модели, получившей название векторной модели атома. Сначала возведем в квадрат уравнение, связывающее J с L и S :

Квадраты моментов можно выразить через соответствующие квантовые числа по уже известным нам правилам. Находим тогда выражение для скалярного произведения

| (5.19) |
Полный магнитный момент атома складывается из магнитного момента, создаваемого суммарным орбитальным моментом количества движения, и суммарного спинового магнитного момента. Но спин, как уже говорилось, обладает двойным магнетизмом. Поэтому с учетом уравнения (5.18) можно записать
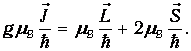
Сокращая общий множитель mB и умножая обе части на

(в правой части J заменен на L + S), получаем
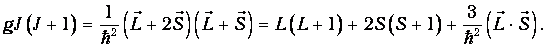
Если подставить сюда выражение (31.19) для скалярного произведения L · S, то получим окончательный ответ
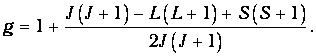
| (5.20) |
Убедимся, что эта формула воспроизводит уже известные результаты. Если полный спиновый момент равен нулю, то полный момент совпадает с орбитальным. Подставляя в (5.20) значения S=0, J=L, получаем g=1, как и должно быть для магнитного момента, создаваемого чисто орбитальным движением электронов. В другом предельном случае нулю равен орбитальный момент, и полный момент количества движения равен спиновому. Подставляя в (5.20) значения L=0, J=S, находим g=2 в полном согласии с двойным магнетизмом спинового момента. Именно такой случай реализуется для элементов первой группы в опыте Штерна-Герлаха. Упоминалось, что для сложных атомов (например, серы) расщепление пучков будет более сложным. Теперь мы можем предсказать результат опыта количественно. Основное состояние серы 3Р2, то есть S=1, L=1, J=2. Из формулы (5.20) для множителя Ланде легко получаем g=3/2, так что магнитный момент атома равен

Проекция магнитного момента на ось z
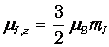
определяется квантовым числом mj проекции полного момента количества движения, которое при J=2 принимает пять различных значений в соответствии с правилами квантования момента:

Теперь, используя решение примера 3 в разделе 5.4, можно рассчитать расщепление пучка атомов серы в опыте Штерна-Герлаха. Ясно, что пучок расщепится на пять компонентов, причем одна из них (mj = 0) не будет отклоняться магнитным полем.
Поиск по сайту: