Прямоугольный барьер конечной ширины

Потенциальный барьер показан на рис. 4.6.

Рис. 4.6. Прохождение частицы над конечным прямоугольным барьером: процесс эквивалентен многократным отражениям от барьера, показанного на рис. 4.5

Решение задачи можно выполнить стандартным образом, записывая суперпозицию плоских волн для каждой из трех областей 1, 2 и 3 и сшивая затем решения, чтобы найти амплитуды волн. Однако мы заменим такой рутинный способ на классическое рассмотрение прохождения волн, что позволит выявить физический смысл получающегося результата.

Заметим прежде всего, что конечный барьер можно рассматривать как наложение двух ступенчатых барьеров, расположенных в точках х=х₀ и х=х₀+d. Это замечание дает возможность использовать ранее полученные формулы.

Пусть волна де Бройля с амплитудой, равной единице, движется слева направо и проникает в область над барьером в точке х₀. Вследствие частичного отражения ее амплитуда уменьшается и становится равной

где D_s - коэффициент прозрачности ступенчатого барьера. Далее она распространяется до точки х=х₀+d, приобретая на пути сдвиг фазы

по сравнению с фазой свободной частицы в этой же точке. Здесь волна снова встречается со ступенчатым барьером, в результате чего ее амплитуда вновь уменьшается до величины

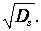
В результате волна выйдет за барьер с амплитудой

(4.44)

Но мы учли только часть волны, выходящей наружу. Пришедшая в точку х=х₀+d волна частично отражается от нее (дополнительный множитель

в амплитуде), идет назад в точку х=х₀, снова отражается там (множитель

в амплитуде), возвращается назад в точку х=х₀+d, где и выходит наружу. Полный пройденный этой частью волны путь равен 3d, дает сдвиг фазы

В результате эта часть волны выйдет за барьер с амплитудой

(4.45)

Аналогичным образом происходят процессы с 2n отражениями внутри барьера, и каждый из них приводит к волне с амплитудой

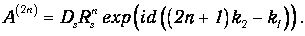
(4.46)

Амплитуда A_r результирующей волны получается суммированием выражения (4.46) по всем п от нуля до бесконечности:

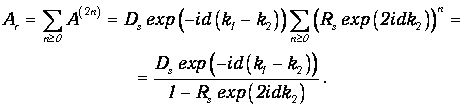
(4.47)

Модуль амплитуды А_г прошедшей над барьером волны даст нам коэффициент прохождения D_r

(4.48)

Подставляя сюда квантово-механическое выражение (4.42) для R_s, получаем

(4.49)

Стандартное решение уравнения Шредингера дает в точности такой же результат. Переходя к оптике, заменяем R_s на выражение (4.43) и k₂ - на wп/с. Получаем тогда коэффициент прозрачности пластины конечной толщины d при нормальном падении света с частотой w:

(4.50)

Это выражение также в точности воспроизводит результат волновой оптики.

Подобным образом можно рассмотреть отраженную от барьера волну, но результат нам уже известен: коэффициент отражения от конечного барьера можно вычислить по формуле

Изучая формулы (4.49) и (4.50), мы обнаруживаем «окна прозрачности» при некоторых значениях частоты падающего света, когда D_r=1; R_s=0, то есть нет никакой отраженной волны. Это случается при

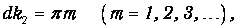
то есть когда четное число полуволн (или целое число волн) света в среде укладывается в двойной ширине барьера:

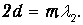
В обратном случае, когда двойная ширина барьера равна нечетному числу полуволн

мы приходим к минимальному значению коэффициента прозрачности

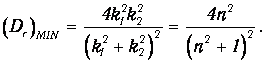
(4.51)

В случае Е<U₀ мы имеем дело с туннелированием - частица «движется» внутри барьера с «мнимым» волновым вектором

(4.52)

В этом случае тригонометрическая функция перейдет в гиперболическую

и из уравнения (4.49) следует выражение для коэффициента прохождения

(4.53)

Если, как это обычно бывает, аргумент

то доминирует член с гиперболическим синусом, причем

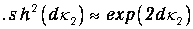
Пренебрегая также предэкспоненциальными множителями, получаем уже знакомое выражение (4.34)

Поиск по сайту: