АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Правило 1

Читайте также:
  1. V2: Спектр атома водорода. Правило отбора
  2. Але монетарне правило не враховує мінливості швидкості обігу грошей та чутливості попиту до зміни процентної ставки.
  3. В/ правило Копа; г/ правило Бергмана.
  4. Виды светофоров и правило их установки
  5. Вопрос 32: «Домашнее хозяйство как экономический субъект. Основные категории и законы потребления. Равновесие потребителя и правило максимизации полезности»
  6. Вопрос№10 Явление электромагнитной индукции. Правило Ленца
  7. Второе правило
  8. Второе правило
  9. Глава VI. Правило фаз.
  10. Гондурасе, Панаме, Парагвае и, как правило, называются На-
  11. Доход и прибыль фирмы. Общий, средний, предельный доход. Экономическая и бухгалтерская прибыль. Правило максимизации прибыли.
  12. Доход и прибыль фирмы. Правило максимизации прибыли.
Классическим динамическим переменным (r, р) в квантовой механике соответствуют операторы - умножение на вектор r, и 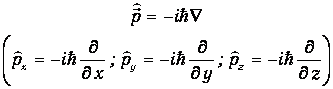- дифференцирование по координатам.

При этом энергии частицы

в потенциальном поле соответствует оператор полной энергии

 
 
 

(4.14)

В этих обозначениях уравнение Шредингера (4.12) имеет вид

 
 
 

(4.15)

Опepaтop полной энергии называется гамильтонианом (аналог функции Гамильтона в теоретической механике).

Напомним, что вклассической механике законы сохранения связаны с симметрией системы: энергия - с трансляцией (сдвигом) времени

импульс - с трансляцией пространства

момент импульса - с поворотами в пространстве (трансляцией углов)

Трансляцию какой-то обобщенной координаты q производит оператор дифференцирования по этой координате. Например, для бесконечно малой трансляции

имеем по определению производной

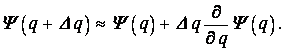
Поэтому не случайно в квантовой механике полной энергии соответствует операция взятия производной по времени

а импульсу - градиент. Аналогично оператор проекции момента импульса на какую-то ось z пропорционален оператору дифференцирования

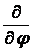
по углу поворота вокруг этой оси:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)