Некоторые следствия соотношений неопределенностей

· Отсутствие траекторий частиц. Для нерелятивистской частицы p=mv и Для массивных объектов правая часть исчезающе мала, что позволяет одновременно измерить скорость и положение объекта (область справедливости классической механики). В атоме же Бора импульс электрона и неопределенность положения оказывается порядка радиуса орбиты. · Невозможность состояния покоя в точке минимума потенциальной энергии.

Например, для осциллятора (тело на пружине) энергию Е можно записать в виде

Основное состояние в классической механике:

Поэтому величина неопределенностей Dр и Dх имеет порядок самих значений импульса и координат, откуда получаем

Минимум энергии достигается в точке

и равен

Вообще говоря, такие оценки не могут претендовать на точный ответ, хотя в данном случае (как и для атома водорода) он действительно точен. Мы получили так называемые нулевые колебания: квантовый осциллятор, в отличие от классического, не может оставаться в покое - это противоречило бы соотношению неопределенностей Гейзенберга. Точные расчеты показывают, что формулу Планка для уровней энергии осциллятора надо было бы писать в виде

где n=0, 1, 2, 3,... - колебательное квантовое число.

При решении задач на применение соотношения неопределенностей следует иметь в виду, что в основном состоянии в классической физике электрон покоится в точке, соответствующей минимуму потенциальной энергии. Соотношения неопределенностей не позволяют ему это делать в квантовой теории, так что электрон должен иметь некоторый разброс импульсов. Поэтому неопределенность импульса (его отклонение от классического значения 0) и сам импульс по порядку величины совпадают

Неопределенность координаты электрона, замкнутого в объеме V, равна по порядку величины линейному размеру этого объема

Пример 1. Электрон с кинетической энергией К=15 эВ находится на металлической пылинке диаметром d=1 мкм. Оценим относительную неточность dv, с которой может быть определена скорость электрона.

По условию

и

Энергия электрона много меньше его энергии покоя, так что можно применять нерелятивистские соотношения

откуда

Для относительной неопределенности скорости электрона получаем

В этом выражении выделены безразмерные множители - отношение комптоновской длины волны электрона

к диаметру пылинки и отношение энергии покоя электрона к его кинетической энергии. Подставляем численные значения:

Пример 2. Среднее время жизни атома в возбужденном состоянии t=10^-8 с. При переходе в основное состояние излучается фотон с длиной волны l=0.5 мкм (зеленый цвет). Определим энергию кванта, ширину и относительную ширину спектральной линии.

Энергия кванта равна

Неопределенность в энергии определяется по соотношению

откуда

Тогда

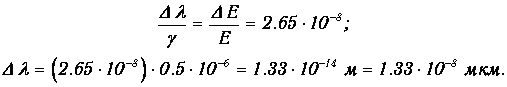
Поиск по сайту: