Классические результаты для теплового излучения

Несмотря на детальное изучение характеристик теплового излучения, математический вид функций f(w, Т) и u(w, Т) долгое время оставался для физиков загадкой.

Попытка строгого теоретического вывода зависимости f(w, Т) принадлежит английским ученым Дж. Рэлею и Дж. Джинсу. Воспроизведем их аргументы. Пусть полость представляет собой прямоугольный ящик с линейными размерами L_x, L_y, L_z вдоль соответствующих координатных осей. Рассмотрим стоячие электромагнитные волны вдоль оси х. Эти волны эквивалентны стоячим волнам, возникающим в струне. Их длины волн l должны удовлетворять соотношению

откуда для проекции волнового вектора находим

Число p нумерует разные типы волн, существующих на струне длины L_x. Поэтому число типов стоячих электромагнитных волн с проекциями волнового вектора в интервале от k_x до k_x+dk_x равно

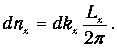
(1.12)

Мы уменьшили результат в два раза, потому что стоячие волны с волновыми числами k_x и -k_x — это одно и то же колебание (направления распространения для стоячих волн не существует).

Аналогичные формулы можно записать для стоячих электромагнитных волн вдоль осей y и z:

(1.13)

Перемножая эти уравнения, находим полное число типов колебаний в прямоугольной полости, волновые векторы которых лежат в интервале от k до k + dk:

(1.14)

Здесь мы увеличили результат в два раза, чтобы учесть поперечность электромагнитных волн: при данной длине волны колебания могут осуществляться в двух взаимно ортогональных направлениях.

Используя сферические координаты, можем записать:

(1.15)

Учитывая, что

получаем (опуская знак «минус»)

(1.16)

Произведение

есть объем полости. Находим тогда для числа типов колебаний, приходящихся на единичный объем:

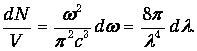
(1.17)

Далее Рэлей и Джинс применили классическую теорему о равнораспределении энергии по степеням свободы, согласно которой на каждую степень свободы в классической статистической системе приходится энергия

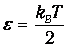
(здесь k_B — постоянная Больцмана). У гармонического осциллятора средняя кинетическая энергия равна средней потенциальной, и поэтому его средняя энергия равна k_BТ. Аналогично в электромагнитной волне колеблются векторы напряженностей электрического и магнитного поля, которые дают одинаковый вклад в средний поток энергии. Поэтому для спектральной плотности энергии излучения Рэлей и Джинс нашли выражения:

(1.18)

Соответственно, для испускательной способности абсолютно черного тела были получены соотношения:

(1.19)

Для длинных волн формула Рэлея — Джинса дает хорошее совпадение с экспериментальными данными, но для коротких волн, то есть в области больших частот, расчетные значения спектральной плотности r*_w перестают совпадать с экспериментом (кривая уходит на бесконечность). Кроме того, энергетическая светимость черного тела также получается бесконечной:

(1.20)

Создавшееся положение было названо «ультрафиолетовой катастрофой». Таким образом, классическая физика оказалась не в состоянии объяснить важные экспериментальные данные.

Закон излучения Планка

М. Планк указал выход из создавшегося положения, выдвинув гипотезу, что электромагнитная энергия испускается и поглощается не непрерывно, а отдельными порциями (квантами)

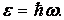
Коэффициент пропорциональности в соотношении между энергией e и частотой света w имеет в СИ размерность [ Дж · с ] и называется теперь постоянной Планка. Впоследствии установили ее численное значение:

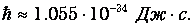
В соответствии с этим приходится принять, что энергия любой колебательной системы, излучающей электромагнитные волны, может принимать лишь дискретный набор значений

кратных собственной частоте колебаний.

Исходя из гипотезы о квантовании энергии колебаний, Планк получил аналитическое выражение для испускательной способности черного тела. Для излучения в состоянии равновесия по-прежнему применяется распределение Больцмана. Вероятность Р_n того, что энергия колебания с частотой w равна

определяется формулой

(1.21)

Сумма всех вероятностей равна единице, откуда мы находим нормировочный коэффициент С:

(1.22)

Средняя энергия колебания с частотой w равна

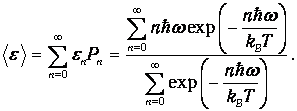
(1.23)

Метод расчета таких сумм основан на выражении для суммы членов геометрической прогрессии и формулы, получаемой из нее дифференцированием:

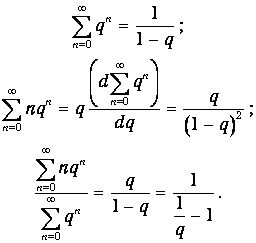
(1.24)

Подставляя сюда

находим выражение для средней энергии колебания

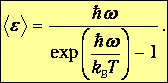
(1.25)

Умножая число колебаний в единице объема на среднюю энергию колебания (1.25), получаем формулу Планка для спектральной плотности энергии теплового излучения

(1.26)

Испускательная способность абсолютно черного тела с учетом формулы (1.6) описывается законом Планка

(1.27)

При высоких температурах (малых частотах)

поэтому экспоненту в знаменателе формул (1.25) и (1.27) можно разложить в ряд:

откуда получаем классическое выражение для средней энергии осциллятора

и формулу Рэлея — Джинса (1.19). Для спектральной плотности энергии и испускательной способности абсолютно черного тела в зависимости от длины волны l имеем

(1.28)

Оказалось, что закон Планка точно согласуется с экспериментальными данными во всем интервале длин волн, в то время как формула Рэлея - Джинса, как уже говорилось, соответствует данным опыта только при больших длинах волн (рис. 27.4).

Рис. 1.4. Сравнение испускательной способности черного тела r_l, МВт/см³ при Т=2 500 К согласно закону Планка и эксперименту(1) и формуле Рэлея—Джинса (2)

Более того, из закона Планка непосредственно получается закон Стефана—Больцмана:

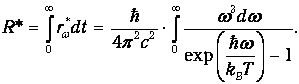
(1.29)

Введем безразмерную переменную интегрирования

В результате этого получаем

(1.30)

Используя значение интеграла

находим аналитическое выражение для постоянной Стефана—Больцмана:

(1.31)

величина которой согласуется с приведенными экспериментальными данными.

Из закона Планка следует также закон смещения Вина. Если продифференцировать функцию Планка (1.28) по l, и приравнять нулю производную, то можно найти положение максимума функции r_l*. Действительно, приравнивая нулю функцию dr_l* / dl, получаем

(1.32)

Введя безразмерную переменную

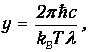
приходим к уравнению

(1.33)

Корень этого уравнения

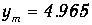
позволяет получить закон смещения Вина:

(1.34)

Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе все эмпирические законы теплового излучения, а также позволяет вычислить константы в этих законах.

Мы искали максимум функции r_l* по длинам волн. Но излучение черного тела можно характеризовать также и распределением (1.27) r_w* по частотам. Найдем для сравнения максимум этого распределения. Для этого надо найти экстремум функции (1.27):

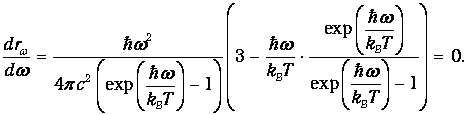
(1.35)

Вводя безразмерную переменную

получаем уравнение для точки максимума распределения r_w*:

(1.36)

которое имеет корень

Отсюда следует, что максимум интенсивности r_w* приходится на частоту

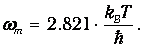
(1.37)

Этой частоте соответствует длина волны

(1.38)

которая, конечно, не определяет максимум функции (1.28) и поэтому не совпадает с выражением (1.34) для l_m из закона смещения Вина:

(1.39)

Пример 1. Принимая, что Солнце излучает как абсолютно черное тело, вычислим его энергетическую светимость и температуру поверхности. Солнечный диск виден с Земли под углом q=32'=9.3·10^-3 рад. Поток солнечной энергии на земной орбите (так называемая солнечная постоянная) равен С=1.4 кВт/м².

Пусть радиус Солнца равен r_C, а расстояние до Земли есть l_З. Их отношение связано с угловым диаметром Солнца:

(1.40)

Если энергетическая светимость Солнца есть R, то полная энергия, излучаемая Солнцем в единицу времени, равна произведению R на площадь поверхности Солнца:

(1.41)

Эта энергия достигает орбиты Земли, где она распределяется по большей площади 4pl_З². Отсюда находим солнечную постоянную

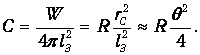
(1.42)

В итоге получаем

(1.43)

По формуле Стефана—Больцмана находим температуру верхних слоев Солнца

(1.44)

Пример 2. В пророчестве Исайи (Ис. 30, 26) сказано:
«И свет луны будет, как свет солнца, а свет солнца будет светлее всемеро, как свет семи дней, в тот день, когда Господь обвяжет рану народа Своего и исцелит нанесенные ему язвы».

Оценим температуру окружающей среды в этот день.
Поток солнечного излучения, падающий на Землю, компенсируется энергией, излучаемой Землей. Из условия задачи следует, что в указанный день поток энергии (с учетом света Луны) в восемь раз превысит нынешний поток солнечного излучения. В состоянии теплового равновесия во столько же раз должен увеличиться поток тепловой энергии с Земли. Из закона Стефана— Больцмана следует, что температура на Земле должна возрасти в

Если нынешняя средняя температура составляет 17°С=290 К, то при увеличении потока энергии в 8 раз она составит Т=1.68·290=487 К=214°С. Жарко будет!

Пример 3. Исходя из данных примера 1, найдем длину волны, на которую приходится максимум энергии солнечного излучения.
Выше была найдена температура верхних слоев Солнца. По закону смещения Вина получаем

ФОТОНЫ

В физике всегда так бывает: скажешь «А» в одном месте - приходится говорить «Б» в другом, даже если не очень хочется. Планк сделал свое сообщение 14 декабря 1900 г., так что XX в. начался с рождения теории квантов. Основная идея Планка: всякий резонатор, излучающий волны с частотой w, может испускать лучистую энергию лишь порциями, кратными минимальному «кванту энергии»

Но физики и предположить тогда не могли, что успешное разрешение проблем с тепловым излучением приведет к ломке многих казавшихся незыблемыми представлений. И первой «пострадала» электродинамика Фарадея - Максвелла, эта «священная корова» классической физики, ее наивысшее достижение.

Поиск по сайту: