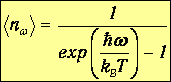ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ

В этой главе речь пойдет о физических принципах работы квантовых усилителей и генераторов оптического излучения. Принципиальная возможность функционирования таких устройств была отмечена в 1939 г. В.А. Фабрикантом, который обратил внимание на способность среды с инверсной населенностью уровней усиливать проходящее через нее излучение. Первые квантовые генераторы, работающие в диапазоне сантиметровых волн (мазеры), были созданы в 1953 г., а в 1960 г. был создан первый аналогичный прибор, работающий в оптическом диапазоне длин волн (лазер). Название этих приборов происходит от заглавных букв английских слов: «мазер» - Microwave Amplification by Stimulated Emission of Radiation (усиление микроволн с помощью вынужденного излучения), «лазер» - Light Amplification by Stimulated Emission of Radiation (усиление света с помощью вынужденного излучения). В 1964 г. Н. Басову, А. Прохорову и Ч. Таунсу за фундаментальные работы в области квантовой электроники, которые привели к разработке генераторов и усилителей нового типа - мазеров и лазеров, была присуждена Нобелевская премия.

Вывод формулы М. Планка по А. Эйнштейну

Ранее мы обсудили, что атомы и ансамбли атомов могут находиться в различных состояниях, характеризуемых набором квантовых чисел. Переход из одного энергетического состояния Е_п в другое Е_т сопровождается поглощением или испусканием кванта электромагнитного излучения - фотона, обладающего энергией

где w - частота излучения. Если Е_п>Е_т, то мы имеем дело со спонтанным (самопроизвольным) переходом атома с более высокого на более низкий уровень, в результате чего испускается фотон с энергией

Схематически этот процесс спонтанного излучения можно изобразить в виде «реакции»

где звездочка указывает на возбужденное состояние атома А.

Если же Е_п<Е_т, то мы имеем дело с вынужденным переходом, сопровождающимся поглощением фотона, энергия

которого идет на увеличение энергии атома (перевод его на более высокий, возбужденный уровень):

В 1918 г. А. Эйнштейн обратил внимание на то, что существуют и «испускательные» переходы другого типа, которые происходят под действием внешнего электромагнитного излучения и вероятность которых возрастает с увеличением интенсивности излучения. В таком процессе фотон падает на возбужденный атом и заставляет его перейти в низшее состояние с излучением другого фотона. В конечном итоге в системе оказывается два фотона - начальный и излученный:

Возникающее в результате таких переходов излучение называется вынужденным или индуцированным излучением. Спонтанное излучение хаотично по направлениям и фазам испускаемых фотонов, так как излучающие атомы независимы. Индуцированное же излучение должно быть по своим характеристикам совершенно тождественно с тем внешним излучением, которое, проходя через вещество, его породило. А именно: индуцированное излучение имеет ту же частоту, направление и поляризацию, что и вынуждающее внешнее излучение. Фазы испускаемых фотонов скоррелированы с вынуждающими колебаниями, то есть индуцированное излучение когерентно.

Вероятности всех трех типов процессов (поглощения, спонтанного и вынужденного излучений) рассчитываются в квантовой электродинамике. Во времена Эйнштейна эта теория еще не была создана, и он применил для анализа проблемы наглядные термодинамические соображения. Далее мы для простоты рассмотрим набор из N атомов, имеющих всего два уровня энергии Е₁ и Е₂ (Е₂>Е₁) - так называемую двухуровневую среду. Пусть в момент времени t какие-то N₂ из общего числа атомов находятся в более высоком энергетическом состоянии 2, и пусть вероятность спонтанного излучения отдельного атома в единицу времени равна А₂₁. Тогда изменение числа атомов в состоянии 2 за малое время dt составит

Знак минус указывает на убыль числа атомов на уровне 2. Величина А₂₁ называется коэффициентом Эйнштейна для спонтанного излучения. Теперь интегрированием легко получаем

(6.1)

где N₂(0) - число атомов в состоянии 2 в начальный момент времени. По смыслу формулы величина

есть среднее время жизни атома в возбужденном состоянии (то есть время, за которое число возбужденных атомов уменьшится в е раз). Этот параметр определяет вероятность процесса спонтанного излучения для данного типа атомов.

Представим теперь, что атомы находятся в равновесии с излучением частотой

и спектральной плотностью энергии u(w, Т) (плотностью энергии в единичном интервале частот). Спектральная плотность энергии пропорциональна числу фотонов данной частоты. Чем больше фотонов, тем вероятнее поглощение одного из них атомом. Поэтому для вероятности процесса вынужденного поглощения излучения атомом в единицу времени можно написать выражение

(6.2)

где коэффициент Эйнштейна В₁₂ характеризует свойства данного атома. Для числа переходов в возбужденное состояние за время dt имеем

(6.3)

Для вероятности индуцированного излучения Эйнштейн предложил использовать аналогичную формулу

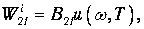
(6.4)

с каким-то другим, вообще говоря, коэффициентом В₂₁. Складывая W₂₁ с вероятностью спонтанного перехода, получаем полную вероятность перехода из состояния 2 в состояние 1 в единицу времени

(6.5)

так что число переходов из возбужденного состояния за время dt равно

(6.6)

При термодинамическом равновесии вещества и электромагнитного поля должен соблюдаться баланс между процессами испускания и поглощения света, то есть равенство полного числа актов испускания света и актов его поглощения. Такое равновесие устанавливается в замкнутой полости, температура Т стенок которой поддерживается постоянной. Если в состоянии равновесия числа переходов 2-1 и 1-2 равны

(6.7)

то мы получаем

(6.8)

Распределение атомов по энергиям при термодинамическом равновесии подчиняется закону Больцмана

(6.9)

откуда

(6.10)

При повышении температуры спектральная плотность энергии должна неограниченно возрастать. Так будет лишь при условии В₂₁=В₁₂, то есть получаем, что коэффициенты Эйнштейна для вынужденного поглощения и индуцированного излучения света равны. Отсюда

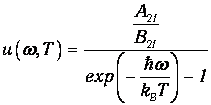
(6.11)

Заметим также, что коэффициенты Эйнштейна не зависят от температуры, ибо относятся к отдельным актам поглощения-испускания фотонов атомом, а температура - это характеристика ансамбля атомов. Тогда в пределе высоких температур мы получаем из (6.11) выражение

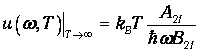
(6.12)

Из сопоставления предыдущей формулы с законом Рэлея-Джинса следует, что

(6.13)

Подставляя (6.13) в (6.11), мы получаем формулу Планка (27.26) для спектральной плотности излучения черного тела. Соотношения между коэффициентами Эйнштейна, выведенные им из простых термодинамических соображений, были подтверждены впоследствии точными расчетами.

Разделив u(w, Т) на число (w²/p²с₃) типов колебаний в единице объема в единичном интервале частот, получаем среднюю энергию одного типа колебания (фотона) частотой w:

(6.14)

Разделив, в свою очередь, это выражение на энергию фотона, находим среднее число фотонов данной частоты при равновесии:

(6.15)

С этой формулой и ее аналогами мы еще встретимся в нашем курсе.

Поиск по сайту: