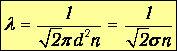Столкновения молекул

Говоря об идеальном газе, мы исходили из того, что молекулы не взаимодействуют между собой. На самом деле предполагалось, конечно, отсутствие потенциальной энергии взаимодействия между ними. Упругие столкновения между молекулами и молекул со стенками обязательно должны происходить хотя бы потому, что иначе будет непонятен механизм, с помощью которого устанавливается равное распределение энергии по степеням свободы, иначе нельзя будет говорить о температуре системы, давлении в ней и т. п. Столкновения молекул происходят случайно. Они приводят к изменению направления и величины скорости частиц, но не меняют распределения молекул по скоростям и координатам в равновесных системах.

Возникает вопрос: а всегда ли молекулы будут сталкиваться друг с другом? Ведь молекулы очень малы, а расстояния между ними в идеальном газе на порядок больше их линейных размеров. Быть может, для сосудов малых размеров они летят без соударений от стенки к стенке? Подсчитаем, сколько раз в единицу времени одна молекула может столкнуться с другими и какое расстояние она пролетает в среднем между столкновениями.

Прежде чем перейти к вычислениям, примем простейшую модель для молекул. Будем представлять их в виде упругих шариков. При столкновении молекул с эффективными диаметрами d₁ и d₂ их центры сближаются на расстояние (d₁+d₂)/2 (рис. 4.1).

Рис. 4.1. Столкновение двух молекул (1) и траектория движения выделенной молекулы газа (2): направление ее движения меняется, когда какая-то из молекул среды попадает в радиус взаимодействия R=(d_t+d₂)/2

Если представить себе, что молекула 1 налетает на молекулу 2, то столкновение произойдет; если первая молекула попадет в сферу радиусом

описанную вокруг второй молекулы. Площадь сечения этой сферы

Величина R называется эффективным радиусом взаимодействия молекул 1 и 2, а s - эффективным сечением взаимодействия этих молекул. При столкновении одинаковых молекул d₁=d₂=d, R=d и

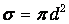
За время между двумя последовательными столкновениями молекула пролетает некоторый путь l. Разумеется, для каждой отдельной молекулы дело чистой случайности, сколь далеко ей удастся продвинуться без столкновений. Но усредняя путь l по всем молекулам системы, получим физическую величину

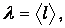
называемую средней длиной свободного пробега молекул. Статистический смысл этой величины таков: отношение малого отрезка длиной dx к l дает вероятность столкновения

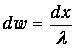
на пути dx. Пусть Р(х) - вероятность пролететь без столкновений расстояние х. Тогда

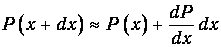
- вероятность, пролететь без столкновений расстояние х+dx. Последнее событие складывается из двух независимых событий:

частица пролетела без столкновений расстояние х (вероятность чего равна Р(х));

частица также без столкновений преодолела еще и маленький отрезок пути dx (вероятность чего равна 1-dx/l). По теореме об умножении вероятностей имеем тогда

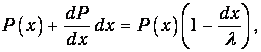
откуда следует уравнение для вероятности Р(х)

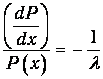
Поскольку вероятность преодолеть нулевое расстояние без столкновений равна единице, имеем дополнительно начальное условие Р(0)=1. Интегрируя дифференциальное уравнение, находим окончательно

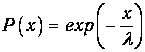
(4.1)

Как видно, чем больше путь х, тем меньше вероятность преодолеть его без столкновений.

Убедимся теперь, что l - действительно средняя длина свободного пробега. Вычислим, с какой вероятностью молекула будет иметь длину свободного пробега l. Это значит, что частица пролетела без столкновений расстояние х=l (вероятность чего есть Р(l)) и столкнулась с другой частицей непосредственно за этим - на малом отрезке длиной dl (вероятность чего можно найти как dl/l). Вероятность dw такого события по теореме умножения вероятностей равна

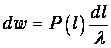
Находим тогда среднюю длину свободного пробега

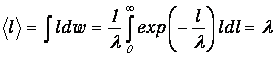
(4.2)

He следует думать, конечно, что вероятность преодолеть расстояние l без столкновений равна нулю: часть молекул может пролететь очень большие расстояния, но лишь крайне небольшая их часть. При х=l, как следует из (4.1), вероятность пролета без столкновений равна

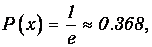
то есть 63.2% частиц испытают столкновения на этом пути. При длине пути х=2l получаем

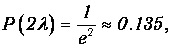
то есть столкновения суждены уже 86.5% частиц, при х=3l в столкновениях участвует уже 95% частиц, поскольку

Чтобы определить среднее число столкновений n одной молекулы с другими в единицу времени, сделаем следующие допущения:

· все молекулы одинаковы, то есть мы не рассматриваем смеси газов;

· все молекулы, за исключением той, за которой мы наблюдаем, неподвижны (в дальнейшем мы покажем, как избавиться от этого заведомо неверного предположения);

· при столкновениях скорость v_ОT молекулы не меняется (это предположение, в сущности, того же уровня, что и предыдущее: при упругом столкновении с препятствием, которое остается неподвижным, модуль скорости действительно не меняется (смысл подстрочного индекса «от» станет ясным в дальнейшем)).

Путь нашей молекулы диаметром d остается прямолинейным до тех пор, пока ей не встретится неподвижная молекула, чей центр окажется от линии движения на расстоянии, меньшем R=d. После этого молекула сменит направление движения и будет двигаться прямолинейно до нового соударения. За интервал времени Dt молекула пройдет ломаный путь v_OTDt и столкнется со всеми молекулами, попавшими в ломаный цилиндр радиусом d и площадью основания s=pd² (см. рис. 4.1). Объем этого цилиндра равен pd²v_OTDt. Если п - концентрация молекул в системе (их число в единице объема), то легко найти количество неподвижных молекул в цилиндре, т о есть число столкновений DN:

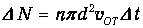
Отсюда следует частота столкновений (то есть число столкновений в единицу времени)

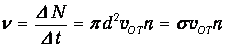
(4.3)

Избавимся теперь от последствий нашего предположения о неподвижности молекул. Пусть мы следим за молекулой 1, которая движется со скоростью v ₁, и она сталкивается с молекулой 2, имеющей скорость v ₂. В системе отсчета, связанной со второй молекулой, она неподвижна, зато первая молекула имеет скорость

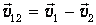
Ясно теперь, что именно среднее значение относительной скорости молекул играет роль скорости v_ОТ, использованной нами при выводе соотношения (4.3) для частоты столкновений. Имеем тогда

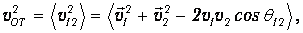
(4.4)

где q₁₂ - угол между направлениями движения молекул. Из-за хаотичности движения этот угол равновероятно принимает любые значения, так что среднее значение его косинуса равно нулю. А усреднение квадратов скоростей приводит к появлению среднеквадратичной скорости молекул

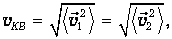
знакомой нам по предыдущей главе. Получаем в итоге, что

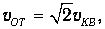
и формула (4.3) записывается в окончательном виде

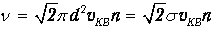
(4.5)

Заметим, что, перейдя от скорости молекулы к ее среднеквадратичной скорости, мы на самом деле избавились и от третьего допущения, поскольку v_KB постоянна при заданной температуре.

Зная частоту столкновений, можно найти среднюю длину свободного пробега. Действительно, время между двумя последовательными соударениями t=1/n, и за это время частица проходит путь l=v_KBt. Таким образом, длина свободного пробега молекулы газа равна

(4.6)

Поскольку при постоянной температуре концентрация частиц пропорциональна давлению, то с ростом давления длина свободного пробега уменьшается. Это и понятно, так как уменьшается среднее расстояние между частицами. На самом деле молекула не является твердым шариком. Поэтому ее эффективный диаметр d - величина не совсем постоянная: он уменьшается при увеличении температуры, хотя и незначительно. Поэтому средняя длина свободного пробега слегка растет с повышением температуры.

Следует отметить, что среднее расстояние между частицами далеко не совпадает со средней длиной свободного пробега. Ранее мы оценили эффективный диаметр молекулы водяного пара d=3 · 10^{-10 м} и среднее расстояние между молекулами при нормальных условиях L=3 · 10^{-9 м}. Отсюда находим концентрацию молекул

Подставляя найденное п в выражение для длины свободного пробега, находим

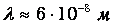
Мы видим, что длина свободного пробега в 200 раз больше диаметра молекулы и в 20 раз больше среднего расстояния между молекулами. Для полноты картины оценим также частоту столкновений. Кинетическая энергия поступательного движения молекулы

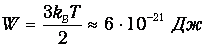
Зная массу молекулы воды

получаем оценку среднеквадратичной скорости

Наконец, определяем

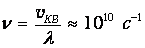
Иначе говоря, молекула испытывает 10 млрд соударений в секунду! Линейный размер сосуда, содержащего один литр газа, равен l=10 см=0.1 м. При скорости 630 м/с молекула могла бы пролететь путь от стенки до стенки за время

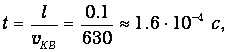
но за это время она испытает

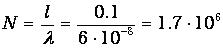
столкновений с другими молекулами.

У нас осталось без обсуждения первое допущение об одинаковости всех молекул. Оно было нужно не по принципиальным соображениям, а для упрощения вывода и окончательных выражений. Если это не так, если мы рассматриваем смесь газов, то компоненты имеют разные концентрации частиц, различные среднеквадратичные скорости, а их молекулы - разные массы. Как следствие, изменится формула для средней длины свободного пробега, причем результаты будут отличаться для различных сортов молекул.

Поиск по сайту: