Теория теплоемкости твердых тел Дебая

П. Дебай предположил, что колебания атомов в кристаллической решетке не являются независимыми. Смещение одного из атомов из положения равновесия влечет за собой смещение соседних с ним атомов. Таким образом, кристалл представляет собой систему N упруго связанных между собой атомов, обладающих 3N степенями свободы. Каждая степень свободы (нормальное колебание) может быть представлена как гармонический осциллятор, среднюю энергию которого <e> мы уже вычислили (см. (7.6)). Из-за связи между атомами частоты нормальных колебаний уже не совпадают между собой. Взаимодействие атомов приводит к тому, что колебание, возникшее в каком-то месте кристалла, передается от одного атома к другому, в результате чего возникает упругая волна. Эта волна, дойдя до границы кристалла, отражается. При наложении прямой и отраженной волн образуется стоячая волна, которой соответствует нормальное колебание кристаллической решетки. Число dN нормальных колебаний, то есть стоячих волн, в интервале частот от w до w+dw велико, поэтому суммирование в выражении для внутренней энергии системы может быть заменено интегрированием:

(7.9)

Число колебаний в единице объема. В этом разделе мы займемся подсчетом числа стоячих волн, имеющих близкие частоты w. В сущности, мы проделали уже эти выкладки ранее для электромагнитного излучения, но повторим их снова с небольшими модификациями для применения также и к упругим колебаниям в кристалле.

Рассмотрим сначала одномерный потенциальный ящик длиной 1_х. Мы могли уже убедиться, что стоячая волна в нем (неважно, электромагнитная ли, звуковая или волна де Бройля), описывается функцией sin (kx), которая должна обращаться в нуль на границах ящика. Отсюда

(7.10)

Число п_х нумерует различные стоячие волны вдоль оси х, и потому на малый интервал волнового вектора dk_х приходится число колебаний

(7.11)

Двойку в знаменателе мы поставили, чтобы избежать двойного счета: замена k_х на - k_х приводит к той же стоячей волне. В трехмерном ящике для волн, распространяющихся по другим осям, получаем аналогичные формулы

(7.12)

Перемножая (7.11) и (7.12), находим для полного числа стоячих волн в ящике объемом V=l_xl_yl_z

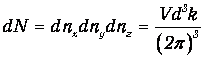
(7.13)

Наконец, учтем, что каждой стоячей волне может соответствовать g поляризаций (для волн де Бройля, соответствующих частицам со спином s, имеем g=2s+1 - число различных проекций спина). Окончательно имеем

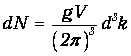
(7.14)

Формула (7.14) дает число различных стоячих волн (отличающихся числом узлов и направлениями поляризации) в объеме V, приходящихся на элемент объема d³k пространства значений волнового вектора. Далее, для перехода к частотам волн вспомним соотношение

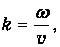
где v - фазовая скорость волны. Отсюда

и окончательно получаем

(7.15)

Мы вывели формулу (7.15) для прямоугольного объема, но можно показать, что форма объема не влияет на результат. Не имеет большого значения и физическая природа колебаний, число которых мы подсчитали. Например, для фотонов v=с и g=2 (свет может иметь правую и левую циркулярные поляризации). В итоге получаем уже известную нам формулу для числа типов фотонов в объеме V в интервале частот dw:

(7.16)

Для применения (7.15) к звуковым волнам в кристалле учтем, что там возможна одна продольная волна, распространяющаяся со скоростью v_||, и две поперечные волны с разными поляризациями, как у фотонов, распространяющиеся со скоростью v _|. Очевидно теперь, как обобщить формулу (7.15) на данный случай:

(7.17)

Здесь мы ввели величину v, играющую роль некого среднего между скоростями продольных и поперечных волн; она вычисляется из соотношения

(7.18)

Характеристическая температура Дебая. Подставляя (7.17) и (7.6) в выражение (7.9) для внутренней энергии, получаем

(7.19)

где w_MAX - максимальная частота нормальных колебаний, которая определяется из соотношения

(7.20)

так как полное число нормальных колебаний равно числу степеней свободы. Используя (7.17), находим

(7.21)

где п - концентрация атомов (их число в единице объема кристалла). Таким образом, максимальная частота нормальных колебаний, называемая дебаевской частотой, равна

(7.22)

Следует отметить, что наименьшая длина упругой волны в кристалле, которая соответствует максимальной частоте w_MАХ, равна

(7.23)

Где
- расстояние между соседними атомами в кристаллической решетке. Этот результат согласуется с тем, что волны, длины которых меньше удвоенного межатомного расстояния, не могут существовать в кристалле.

Используя определение (7.22) и учитывая, что для одного моля кристалла концентрация атомов равна

где п_а - число атомов в молекуле вещества кристалла, мы можем записать внутреннюю энергию одного моля в виде

(7.24)

Дифференцируя внутреннюю энергию U по температуре, можно получить молярную теплоемкость кристалла:

(7.25)

Введем новый параметр - характеристическую температуру Дебая

(7.26)

и выполним в интеграле (7.25) замену переменных

Тогда молярную теплоемкость кристалла можно записать в виде

(7.27)

При низких температурах Т<<q_D верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности. Тогда интеграл будет представлять собой число

и теплоемкость окажется пропорциональной кубу температуры:

(7.28)

Эта приближенная зависимость известна как закон Дебая и хорошо согласуется с экспериментом при достаточно низких температурах Т<<q_D.

При высоких температурах Т>>q_D экспонента в числителе приближенно равна единице, а экспоненту в знаменателе можно разложить в ряд Тейлора:

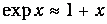
Тогда для молярной теплоемкости получается значение

(7.29)

то есть закон Дюлонга и Пти.

О согласии теории Дебая с опытом можно судить по графику рис. 7.1, на котором показаны экспериментальные точки для некоторых веществ.

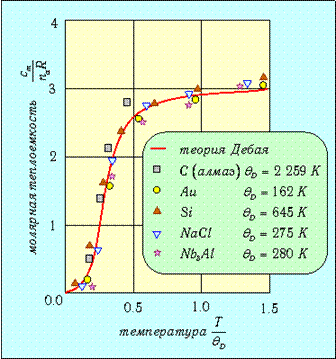
Рис. 7.1.Сравнение теории теплоемкости Дебая с экспериментальными данными: показаны вещества с заметно различающимися значениями дебаевской температуры и разным составом молекул (п_а=2 для NaCl и п_а=4 для Nb₃Al), но все точки лежат достаточно близко от теоретической кривой

Поиск по сайту: