 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Адиабатный процесс
| Адиабатныйпроцесс - это процесс, при котором не происходит теплообмена с внешней средой. |
Физически это означает, что процесс протекает достаточно быстро и система не успевает обменяться теплотой с внешними телами. Однако коль скоро мы имеем дело с равновесными процессами, скорость адиабатного процесса не должна быть слишком уж велика. Примером таких процессов может служить распространение звуковых колебаний в упругой среде.
Выведем уравнение, описывающее адиабатный процесс. Ранее мы имели дело с самыми простыми уравнениями процессов

| - для изотермического процесса; |

| - для изобарного процесса; |
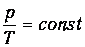
| - для изохорного процесса; |
Поскольку в адиабатном процессе dQ=0, из первого начала термодинамики следует, что

C другой стороны,

Приравнивая эти выражения, находим

| (2.28) |
Умножая уравнение (2.28) на Vg-1, получаем в левой части полный дифференциал

| (2.29) |
В результате интегрирования (2.29) приходим к уравнению адиабатного процесса
| (2.30) |
Графически адиабатный процесс описывается на (р, V)-диаграмме кривыми, похожими на изотермы (рис. 2.5), но идущими круче, так как g>1, поскольку Сp>СV.

Рис. 2.5. Адиабатный процесс в идеальном газе: 1 - адиабата, 2 - изотерма
Это и понятно, так как при адиабатном расширении газ совершает работу за счет внутренней энергии, и его температура падает, что еще больше уменьшает давление по сравнению с изотермическим расширением.
Экспериментальное исследование адиабатного процесса в идеальном газе можно выполнить с помощью установки, представленной на рис. 2.6.

Рис. 2.6. Экспериментальное изучение адиабатного процесса в идеальном газе
Учитывая, что из уравнения состояния идеального газа следует пропорциональность

уравнение адиабатного процесса можно также представить в виде
| (2.31) |
Первый закон термодинамики в применении к адиабатному процессу позволяет вычислить работу газа при адиабатном расширении:

| (2.32) |
Выражения для работы при адиабатном процессе с учетом уравнения Клапейрона-Менделеева можно выразить также через температуры в начале и конце процесса
| (2.33) |
Для бесконечно малых изменений параметров уравнения (2.32), (2.33) переходят в соотношения
Поиск по сайту:


