Пример. Определим, на какой высоте давление кислорода уменьшается в два раза (при Т=300 К)

Определим, на какой высоте давление кислорода уменьшается в два раза (при Т=300 К).

Применяем барометрическую формулу.

Тогда

откуда

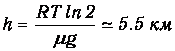
Используя уравнение идеального газа в форме

(3.50)

из барометрической формулы легко получить закон изменения с высотой числа п молекул в единице объема:

(3.51)

Из (3.51) следует, что состав воздуха с ростом высоты будет меняться количественно: возрастет концентрация газов с малой молярной массой, например водорода и гелия.

У поверхности воздух представляет собой смесь газов: N₂ - 78.08%, O₂ - 20.95%, СO₂ - 0.03%, инертные газы - 0.94%. Посмотрим, как изменится относительное количество кислорода к азоту в изотермической атмосфере (Т=300 К) на высоте 10 км.

Отношение концентраций кислорода и азота уменьшится от 0.27 до 0.23. Наш расчет справедлив лишь для изотермической атмосферы и сравнительно небольших высот, для которых ускорение свободного падения изменяется незначительно: g=const, T=const.

Распределение Больцмана. Число молекул в единице объема зависит от высоты h и температуры Т, причем обе переменные входят в показатель экспоненты. Уравнение (3.51) можно записать в виде

(3.53)

где k_B - масса одной молекулы газа. При этом выражение m₀gh, стоящее в числителе, есть не что иное, как потенциальная энергия одной молекулы в поле тяжести Земли. Поэтому можно говорить, что мы имеем распределение молекул по значениям потенциальной энергии. При этом чем больше потенциальная энергия, тем меньше таких молекул. В знаменателе показателя степени стоит k_B - величина, пропорциональная средней энергии теплового движения молекулы. Чем выше температура, то есть чем больше энергия теплового движения молекул, тем экспоненциальный множитель, пропорциональный концентрации молекул, с ростом высоты убывает медленнее. На рис. 3.7 показаны кривые относительной концентрации молекул кислорода O₂ на разных высотах при двух различных температурах Т₁=300 К и Т₂=1 300 К (последний случай, конечно, нереален и используется лишь как иллюстрация).

Рис. 3.7. Зависимость относительной концентрации молекул кислорода от высоты при разных температурах T₁=300 K и T₂=1 300 K

Видно, что число частиц в единице объема при большей температуре медленнее убывает с высотой. При уменьшении температуры большая часть частиц располагается на меньшей высоте. А при Т= 0 все частицы расположились бы на поверхности Земли. Этот факт имеет простое физическое объяснение. Каждое конкретное распределение молекул по высоте устанавливается в результате действия двух тенденций:

· притяжение молекул к Земле, характеризуемое потенциальной энергией m₀gh, стремится расположить их на поверхности Земли;

· тепловое движение, характеризуемое энергией k_BТ, стремится разбросать молекулы по всем высотам равномерно.

Обозначив Е_р=m₀gh, получим

(3.53)

то есть концентрация молекул больше там, где меньше их потенциальная энергия. Это согласуется с общим принципом, которому подчиняется природа. Всякая система стремится занять положение с наименьшей потенциальной энергией. Частицы будут с большей вероятностью располагаться в тех точках пространства, где потенциальная энергия меньше.

Больцман доказал, что такое распределение осуществляется в поле любых сил, а не только в гравитационном поле. Поэтому распределение (3.53), где п - концентрация частиц с потенциальной энергией Е_р называется распределением Больцмана.

Поиск по сайту: