Макроскопические квантовые явления

Не следует думать, будто законы квантовой механики важны только при рассмотрении явлений в масштабах атомов и молекул. При низких температурах вблизи абсолютного нуля существуют и макроскопические проявления этих законов. С ними мы и познакомимся в этом разделе.

Бозе-эйнштейновская конденсация. Рассмотрим идеальный газ свободных бозонов, которые не взаимодействуют ни друг с другом, ни с внешним полем. Состояние частицы задается ее импульсом р и проекцией спина (имеется всего g=2s+1 возможностей, для бозонов s - целое число). Среднее число бозонов в данном состоянии к описывается формулой (7.51). Поскольку принцип запрета Паули на бозоны не распространяется, они могут накапливаться в одном состоянии. При нулевой температуре все частицы системы должны занять нижний энергетический уровень с Е=0. Возникает вопрос, что будет при Т>0?

Снова вспомним формулу (7.14) для числа типов колебаний, но заменим в ней волновой вектор на импульс частицы:

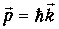
Получаем тогда

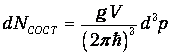
(1)

Индексом «сост» мы хотим подчеркнуть, что, имея дело с квантовыми частицами, мы стали называть вещи своими именами: число колебаний становится в этом случае числом состояний, в которых можно обнаружить частицу. Элемент объема пространства импульсов можно записать в виде

где W - телесный угол. Интегрируя соотношение (1) по углам, получаем число состояний dN_p, в которых модуль импульса частицы заключен между значениями р и р+dp:

(2)

Учитывая, что энергия свободной нерелятивистской частицы

так что

находим из (1) число состояний dN_E с энергиями между E и E+dE:

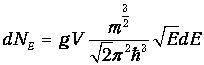
(3)

Умножая (3) на среднее число частиц в одном состоянии, находим число частиц, приходящееся на тот же интервал энергий:

(4)

Чтобы получить полное число частиц в системе, проинтегрируем (4) по всем значениям энергии:

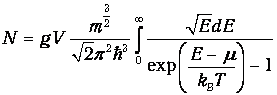
(5)

Вводя новую переменную интегрирования

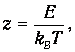
переписываем (5) в виде

(6)

Это - уравнение для химического потенциала m. В сущности, мы переписали формулу (7.52) в виде, удобном для практического применения: суммирование по всем возможным состояниям заменено на суммирование (интеграл) по энергии частицы, а число состояний учтено у нас при использовании формулы (3).

Если при заданной концентрации частиц N/V понижать температуру газа, то химический потенциал будет увеличиваться (то есть уменьшаться по модулю), как следует из (6). Предельного значения m=0 он достигнет при температуре Т₀, определяемой уравнением

(7)

откуда следует выражение

(8)

Разберемся в физическом смысле входящих в формулу (8) комбинаций параметров. Если обозначить через l среднее расстояние между частицами, то в объеме сферы радиусом l/2 будет содержаться одна частица, то есть плотность частиц будет

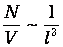
Поэтому формулу (8) можно переписать в виде

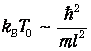
Поскольку тепловая энергия движения частиц

мы получаем отсюда

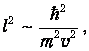
или

где l_В - длина волны де Бройля (мы опустили в этом рассуждении несущественные числовые множители). Таким образом, снова приходим к выводу, что квантовые эффекты становятся заметными, когда длина волны де Бройля имеет порядок расстояния между частицами. Формула (8) - это общее выражение для «квантовой» температуры: оно еще нам встретится, а меняться может лишь числовой множитель.

Итак, при Т>Т₀ существует физически приемлемое (m<0) решение уравнения (6). При Т<Т₀ химический потенциал остается равным предельному значению 0, дальше ему меняться некуда, и правая часть уравнения становится меньше N/V. Этот результат удивителен, ибо число частиц в системе фиксировано, и плотность частиц, казалось бы, должна оставаться неизменной. Стало быть, какая-то доля этих частиц куда-то девается, выпадает из системы, перестает участвовать в тепловом движении. Значит, правая часть (6) будет при Т<Т₀ (m=0) описывать те частицы, которые в тепловом движении участвуют, то есть энергия которых больше нуля:

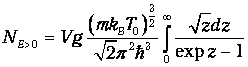
(9)

Если умножить и разделить правую часть (9) на

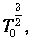
то можно выделить фактор

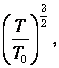
а оставшийся сомножитель, в соответствии с (7), будет равен полному числу N частиц в системе:

(10)

Остальные частицы имеют нулевую энергию; их число N_E=0 определится как разность N - N_E=0:

(11)

Итак, при температуре ниже критической Т<Т₀ происходит так называемая бозе-эйнштейновская конденсация - накопление частиц в состоянии с р =0. Эффект этот - макроскопический, так как число частиц конденсата огромно, порядка полного числа частиц N. При понижении температуры ниже критической конденсат появляется внезапно - система испытывает резкое изменение свойств (как говорят, происходит фазовый переход).

При абсолютном нуле температуры все частицы системы находятся в конденсате. При повышении температуры некоторые из них покидают конденсат и начинают участвовать в тепловом движении. При Т>Т₀ бозе-эйнштейновский конденсат исчезает: в нем не остается частиц. Зависимость доли частиц в конденсате от температуры показана на рис. 1.

Рис. 1. Доля частиц в бозе-эйнштейновском конденсате в зависимости от температуры

Важно отметить, что конденсация происходит не в обычном пространстве, как при выпадении, например, росы, но в пространстве импульсов. С точки зрения нашего обычного пространства и конденсат, и нормальный компонент бозе-газа «размешаны», и система остается пространственно однородной. Но есть и сходство с обычным насыщенным паром: например, при Т<Т₀ давление не зависит от объема системы, что для идеального газа необычно.

Явление, предсказанное Эйнштейном и индийским физиком Бозе много лет назад, впервые экспериментально наблюдалось в 1995 г. в США. «Газ» из 2 000 атомов рубидия, охлажденный почти до абсолютного нуля (20 нК), «сконденсировался» в «суператом», который вел себя уже не как газ частиц, но как единое целое. Таким образом, было создано новое состояние вещества, никогда ранее не существовавшее в естественном виде во Вселенной, как было сказано в со общении об этих работах. В 2001 г. авторам этих экспериментальных работ была присуждена Нобелевская премия.

Явление сверхтекучести. Сверхтекучесть - это свойство жидкого гелия протекать без трения сквозь тонкие капилляры при низких температурах Т<2.17 К. Явление открыто П.Л. Капицей в 1938 г. (Нобелевская премия была присуждена в 1978 г.). Дальнейшие исследования показали, что в жидком гелии как бы имеются два компонента: нормальный и сверхтекучий. Из-за отсутствия вязкости сверхтекучий гелий не оказывает сопротивления погруженным телам. В сверхтекучем состоянии жидкий гелий проявляет так много необычных свойств, что мы вправе считать сверхтекучий компонент особым состоянием вещества, которое принято обозначать Не II (в отличие от обычного Не I). Упомянем лишь так называемый эффект фонтанирования: при освещении карманным фонарем нижнего конца капилляра, опущенного в жидкий гелий, он нагревается и доля сверхтекучего компонента падает. Избыточное давление заставляет втекать в капилляр сверхтекучий компонент, что приводит к появлению фонтанчика высотой до 30 - 40 см. Такое перетекание гелия от холодного места к горячему необычно: в нормальных жидкостях все происходит как раз наоборот.

Фазовая диаграмма для гелия представлена на рис. 2.

Рис. 2.Фазовая диаграмма для ⁴Не (по осям отложены давление и температура). Штрихами показана l-линия между нормальным (Не I) и сверхтекучим (Не II) состояниями

Фазовый переход Не I => Не II происходит на так называемой l- линии, причем температура перехода уменьшается с ростом давления. Сверхтекучее состояние наблюдалось для изотопа ⁴Не (сверхтекучесть у другого изотопа ³Не увидели гораздо позже и с большим трудом, но это - другая история). Поскольку протон и нейтрон, входящие в ядро гелия, имеют спин 1/2, то спин ядра ⁴Не - целый, а ³Не - полуцелый. Здесь возникает разница между бозонами и фермионами. Частицы жидкого ⁴Не - бозоны, и они могут претерпевать конденсацию Бозе-Эйнштейна. К тому же при типичной концентрации частиц в жидкости N/V=2 · 10²⁸ м^-3, массе ядра гелия т=6.7 · 10^{-27 кг} и g=1 (полный спин ядра равен нулю) формула (8) дает для температуры бозе-эйнштейновской конденсации значение T₀=2.9 К, что не так далеко от температуры l- перехода. Представляется весьма соблазнительным связать два необычных состояния вещества - бозе - эйнштейновский конденсат и сверхтекучий компонент. Но все не так просто, как кажется.

Элементы микроскопической теории сверхтекучести. Дело в том, что жидкость - не идеальный газ, там имеется сильное взаимодействие между частицами. А мы рассматривали конденсат в системе идеального газа бозонов. И надо еще разобраться, почему конденсат должен проявлять сверхтекучесть. Согласно микроскопической теории Н.Н. Боголюбова (1947), нельзя говорить о состоянии отдельных атомов гелия, но лишь о состоянии всей системы. Здесь мы впервые встречаемся с квантовой жидкостью - макроскопическим квантовым эффектом. При Т=0 система находится в основном состоянии, при повышении температуры возникают тепловые возбуждения, переход на низколежащие возбужденные уровни энергии. Коллективные возбуждения атомов квантуются аналогично колебаниям атомов кристаллической решетки в теории Дебая. Там при квантовании возникали фононы, здесь - квазичастицы, отдельные кванты с энергией e(р). Оказалось, что первостепенную роль играет закон зависимости энергии от импульса р - закон дисперсии. В квантовой бозе - жидкости «возбуждения» (квазичастицы) - также бозоны с нулевым спином. При низких температурах число квазичастиц мало, и их можно считать невзаимодействующими. В этом случае имеем идеальный газ квазичастиц, который при какой-то критической температуре испытывает конденсацию.

Но все, повторим, зависит от закона дисперсии, полный расчет которого очень сложен и до сих пор не выполнен. Боголюбов вычислил дисперсию слабовозбужденных состояний. В предельных случаях его формула дает

(12)

где v - некая постоянная с размерностью скорости. Энергия в первом случае есть не что иное, как энергия атома гелия. Энергия же во втором предельном случае аналогична энергии акустического кванта (фонона). Ход кривой показан на рис. 3.

Рис. 3.Зависимость энергии квазичастиц в Не II от их импульса (закон дисперсии)

Таким образом, при T>0 жидкий гелий состоит из конденсата квазичастиц и идеального газа квазичастиц с энергией e(р). Атомы гелия нельзя разделить на «образующие конденсат» и «порождающие свободные квазичастицы»: все они принимают участие в образовании как основного конденсатного состояния, так и идеального газа. Газ квазичастиц может рассматриваться как нормальный компонент жидкого гелия, а конденсат - как сверхтекучий. Подобная феноменологическая теория двухкомпонентной жидкости была развита Ландау (1941).

Сверхтекучесть конденсата. Мы разобрались, почему в жидкости может появиться идеальный газ: свободные частицы газа - это не сами атомы гелия, но возбуждения основного состояния (конденсата). Теперь надо понять происхождение сверхтекучести конденсата.

Сначала напомним результаты классической механики, касающиеся перехода к движущимся системам отсчета. Пусть дана система К, в которой радиус - векторы частиц с массами m_i обозначены r _i. Импульс такой системы есть

а кинетическая энергия

где

Пусть дана также система К’, положение начала координат которой задается вектором R, скорость системы К’ относительно К есть

В движущейся системе координат радиус - векторы частиц есть

Отсюда немедленно следуют выражения для полного импульса и энергии частиц в движущейся системе координат (М - полная масса всех частиц):

(13)

Это - нерелятивистские преобразования Галилея, известные из классической механики. Следуя рассуждениям Ландау, применим теперь эти формулы к невозбужденному конденсату, текущему по трубке со скоростью V. В лабораторной системе отсчета К энергия и импульс конденсата даются очевидными формулами

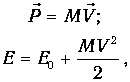
(14)

где Е₀ - энергия покоящегося конденсата в основном состоянии. Возьмем систему К’, движущуюся со скоростью конденсата V, так что в ней конденсат покоится. Преобразования Галилея (12) тогда дают

(15)

Эти результаты очевидны, и мы напомним только, что все это относится к конденсату в основном состоянии. В системе К’ он покоится, а мимо него со скоростью -V движется трубка. Если есть вязкость, то она проявится в диссипации энергии. Это не может сразу произойти во всей жидкости: сначала возбудятся отдельные внутренние движения, появятся квазичастицы типа фононов. Пусть возникло возбуждение с импульсом р и энергией e(р). Для возбужденного конденсата в К’ имеем вполне очевидные соотношения

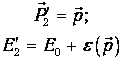
(16)

Как эти формулы будут выглядеть в лабораторной системе отсчета? Чтобы перейти назад в К, используем обратные преобразования Галилея:

(17)

откуда находим

(18)

Сравнивая формулы (14) и (18), находим изменение энергии движущегося конденсата в лабораторной системе К при переходе из основного состояния в возбужденное:

(19)

Образование квазичастицы энергетически выгодно, если DЕ<0. В самом благоприятном для этого случае импульс р антипараллелен скорости V, и изменение энергии конденсата равно

Отсюда следует, что для торможения жидкости необходимо выполнение условия

(20)

Здесь мы ввели обозначение и* для параметра с размерностью скорости - отношения минимума энергии возбуждения к импульсу. Этот параметр равен тангенсу угла наклона штриховой линии на рис. 3. Если спектр возбуждений таков, что и*>0, как это и показано, то условие торможения не выполняется при слабых возбуждениях: как говорят, в спектре возбуждения имеется энергетическая щель - некая разность между энергией возбуждения и энергией основного состояния. Это значит, что при малых скоростях V<и* трение невозможно. Иными словами, мы получили явление сверхтекучести (при малых импульсах скорость и* равна скорости звука). Смысл полученного результата в том, что конденсат - это коллективное образование, реагирующее на выпадение одного из своих членов повышением энергии, в то время как трение должно энергию понижать. Закон дисперсии, изображенный на рис. 3, таков, что условие сверхтекучести выполнено. Для обычных бозе-частиц с

имеем

и условие сверхтекучести не выполнено.

Вывод: обычные частицы даже в конденсатном состоянии сверхтекучестью не обладают, конденсат не образует связанного коллектива и не реагирует на замедление отдельных частиц.

Еще раз подчеркнем: Не II - не смесь различных веществ, и его компоненты невозможно выделить по отдельности. Лучше было бы говорить об одновременном сосуществовании в гелии не компонентов, а двух видов движения - нормального и сверхтекучего.

Сверхпроводимость. В 1911 г. голландский физик Г. Камерлинг-Оннес открыл удивительное явление. При температуре около 4 К электрическое сопротивление ртути скачком уменьшалось до нуля. Впоследствии явление сверхпроводимости было обнаружено им у олова, свинца, таллия и других веществ. Были проведены многочисленные эксперименты по выявлению свойств сверхпроводящего состояния вещества.

Важнейшими свойствами сверхпроводящего состояния вещества являются:

· наличие критической температуры Т_с, при которой возникает сверхпроводящее состояние;

· выталкивание слабого магнитного поля из толщи сверхпроводника за исключением тонкого слоя вблизи его поверхности (эффект Мейснера);

· разрушение сверхпроводящего состояния при наложении достаточно сильного магнитного поля;

· необычная температурная зависимость теплоемкости сверхпроводника.

Для большинства известных ранее веществ критические температуры имеют порядок 1 - 15 К. В 1986 г. были открыты керамические соединения, переходящие в сверхпроводящее состояние при температурах порядка 125 К, то есть выше точки кипения жидкого азота. Поскольку ранее сверхпроводники получались лишь при охлаждении материала жидким гелием, а жидкий азот гораздо дешевле в производстве, открытие высокотемпературной сверхпроводимости сулит развитие многочисленных технических приложений.

Критическое значение индукции магнитного поля В_с, при котором происходит разрушение сверхпроводящего состояния, зависит от температуры сверхпроводника. Характерный график зависимости показан на рис. 4; он хорошо описывается формулой

(21)

где В₀ - критическое значение поля при абсолютном нуле температуры.

Рис. 4. Значение критического магнитного поля как функция температуры сверхпроводника

Как мы увидим далее в нашем курсе, теплоемкость нормального металла при низких температурах имеет вид

(22)

где первое слагаемое - уже знакомый нам вклад кристаллической решетки, описываемый теорией Дебая, а второе слагаемое - изучаемый в следующей части курса вклад электронного газа. В сверхпроводнике теплоемкость при очень низких температурах определяется, как показывают эксперименты, выражением типа

(23)

Первое слагаемое не изменилось: кристаллическая решетка по-прежнему на месте. Драматическое изменение второго слагаемого (экспонента вместо линейной функции) показывает, что сверхпроводимость связана с какими-то коренными изменениями поведения электронов проводимости.

Микроскопическая теория сверхпроводимости была создана Д. Бардиным, Л. Купером и Д. Шрифером и усовершенствована Н. Н. Боголюбовым. Она слишком сложна для изложения в данном учебнике. Достаточно лишь указать на то, что имеется глубокая аналогия между сверхтекучестью и сверхпроводимостью. Из-за взаимодействия электронов с фононами между электронами возникает притяжение, и при определенных условиях может образоваться своеобразное связанное состояние - куперовская пара электронов с противоположными спинами. Такое образование является уже бозоном и может испытывать бозе - эйнштейновскую конденсацию, что и является предпосылкой перехода материала в сверхпроводящее состояние.

При абсолютном нуле температуры электронный газ в сверхпроводнике переходит в основное состояние, обладающее свойствами конденсата. Что очень важно, это состояние отделено энергетической щелью Е от следующего, возбужденного, состояния. Иначе говоря, чтобы вывести электрон из основного состояния, надо придать ему некоторую минимальную энергию Е_g, а меньшие порции энергии просто не будут восприняты. Нечто подобное мы уже видели для сверхтекучего состояния, а еще ранее - для теплоемкости («замораживание» вращательных и колебательных степеней свободы, теория теплоемкости Эйнштейна). Теория предсказывает простую связь энергетической щели и критической температуры:

Наличие энергетической щели сразу объясняет поведение теплоемкости электронного газа. Действительно, энергия Е_g - это минимальная энергия, разрушающая куперовскую пару, и сообщение такой энергии порождает пару свободных электронов. Тогда на каждый электрон приходится половинная энергия E_g/2. Из статистических соображений можно утверждать, что число электронов вне основного состояния пропорционально величине

Тепловая энергия, поглощаемая при возбуждении, пропорциональна

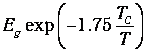
Производная этой величины по температуре дает теплоемкость электронного газа в сверхпроводящем состоянии:

(24)

При низких температурах предэкспоненциальный множитель 1/Т² меняется гораздо медленнее экспоненты, так что этот закон практически не отличается от феноменологического соотношения (23). При изменении температуры величина щели изменяется по закону, похожему на изображенный на рис. 4. При критической температуре щель исчезает, и вместе с ней исчезают сверхпроводящие свойства. Заметим, что выражение (24) аналогично формуле для теплоемкости (7.8) в теории Эйнштейна, где также имеется щель между основным и возбужденным уровнями энергии.

Из сказанного ясно, какую важную роль играет энергетическая щель. В системе бозонов она ответственна за явления сверхтекучести и сверхпроводимости. В системе фермионов, как мы увидим в дальнейшем, она ответственна за различие свойств металлов, диэлектриков и полупроводников.

Исследования явлений сверхтекучести и сверхпроводимости всегда вызывали большой интерес как ученых, так и общества в целом. «Виной» тому - широкие перспективы их практического использования. Особое значение они приобретают в современном мире, где ученые научились создавать совершенно новые материалы с необычными характеристиками, проявляющие, например, сверхпроводящие свойства при относительно высоких температурах и в достаточно сильных магнитных полях. Не случайно за исследования в этой области присуждена не одна Нобелевская премия, начиная с Камерлинг-Оннеса (премия 1913 г.) и заканчивая пока премией 2003 г., которую получили А.А. Абрикосов (Россия и США), В.Л. Гинзбург (Россия) и Э. Леггетт (Великобритания и США).

Поиск по сайту: