Распределение молекул по скоростям

В этом разделе, являющемся центральным для данной темы, устанавливается вид так называемого распределения Максвелла.

Газ, предоставленный самому себе и находящийся в постоянных внешних условиях, приходит в состояние равновесия. С макроскопической точки зрения в нем устанавливаются постоянная температура и постоянное давление. Если газ состоит из нескольких компонентов (как, например, воздух), то и состав газа в разных местах в сосуде будет одинаков. Молекулы газа даже в равновесии движутся беспорядочно, сталкиваясь между собой и со стенками сосуда, беспрерывно меняя свою скорость. Однако не все столь хаотично, как кажется на первый взгляд. Как бы ни изменялись скорости отдельных молекул, среднее значение квадрата скорости, как это следует из формулы (1.14) молекулярно-кинетической теории идеальных газов) остается постоянным и равным

(3.6)

Зададим вопрос: сколько молекул (или лучше, какая доля молекул) движется с определенной скоростью в данный момент? Из предположения о хаотическом характере молекулярного движения следует, что возможно появление молекул с любыми скоростями, так что распределение молекул по скоростям надо характеризовать непрерывной функцией. Несмотря на полную хаотичность молекулярных движений, несмотря на случайный характер столкновений и вызываемых ими изменений скоростей молекул, их распределение по скоростям, как показывают теория и опыт, оказывается вполне определенным. На характер распределения по скоростям не влияют даже внешние поля при условии, что состояние системы является равновесным.

Будем считать, что возможные значения скорости заключены в интервале от 0 до бесконечности. В реальных системах скорость не может быть бесконечно большой, так как всякая система состоит из большого, но конечного числа молекул. Поэтому даже если представить себе такой практически невероятный случай, при котором все молекулы остановятся, передав всю энергию одной единственной молекуле, то и тогда энергия этой молекулы и, следовательно, ее скорость будет конечной. Мы здесь даже не говорим об ограничениях, налагаемых теорией относительности, согласно которой скорость любой молекулы не может превысить скорость света. Очень малые и очень большие по сравнению со средним значением скорости мы будем считать в принципе возможными, но, как мы убедимся, они окажутся маловероятными.

Итак, найти распределение молекул по скоростям - это означает определить, сколько молекул или какая доля молекул из общего числа N обладают скоростями, лежащими в интервале от v до v+Dv.

Функция распределения молекул по скоростям. Если DN - число молекул, имеющих при заданном состоянии системы скорости от v до v+Dv, то это число, вообще говоря, зависит от:

· общего числа молекул N в системе;

· величины интервала Dv;

· значения самой скорости v (так как в одинаковых по величине интервалах, но при разных абсолютных значениях скорости число частиц будет различным).

Таким образом,

Здесь под v понимается вектор с компонентами (v_x, vy v_z) (в декартовой системе координат). Кроме того, нам понадобится величина

то есть «объем» интервала скоростей.

При неограниченном уменьшении этого «объема» число частиц в нем, естественно, стремится к нулю. В таких случаях, как было пояснено выше, необходимо пользоваться другой функцией (мы обозначим ее буквой F), численно равной количеству молекул, приходящемуся на единичный объем интервала скоростей:

(3.7)

Неограниченно уменьшая D v, переходим в пределе к дифференциальной величине

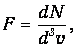
(3.8)

где бесконечно малый объем скоростей

Функция F зависит уже лишь от N и v:

Зависимость от конечного интервала скоростей может быть получена обратной операцией - интегрированием.

Обратимся теперь к зависимости функции F от числа молекул в системе. Чем больше полное число N молекул, тем больше число молекул DN, приходящееся на единичный объем интервала скоростей. В пределе очень большого числа молекул, когда

величина F пропорциональна рассматриваемому количеству молекул N и, следовательно, для различных порций газа будет различна. Поэтому рассмотрим другую функцию:

(3.9)

Эта функция зависит лишь от скорости и дает относительное количество (долю) молекул, имеющих скорость в единичном интервале скоростей вблизи скорости v. Эта функция n(v) называется функцией распределения молекул по скоростям. Если взять несколько порций одного и того же газа, находящихся в идентичных условиях (одинаковы р и Т), то распределение молекул по скоростям в них также будет идентично. Зная вид n(v), можно найти количество молекул dN из общего числа молекул N, скорости которых попадают внутрь интервала dv, то есть имеют значения, заключенные в пределах от v до v+dv:

Исходя из определения вероятности, мы можем заключить, что величина

является вероятностью того, что любая из молекул газа обладает скоростью, лежащей в интервале dv вблизи v, а сама функция n( v ) имеет смысл плотности вероятности.

Функция распределения должна подчиняться условию, имеющему простой физический смысл: число молекул с произвольными значениями скорости от 0 до бесконечности в объеме V равно полному числу молекул N, находящихся в этом объеме. Если просуммировать числа DN( v ) по всем скоростям от 0 до бесконечности, то эта сумма должна равняться полному числу молекул N. Для более точных вычислений нужно брать интервалы бесконечно малыми, а сумму заменить интегралом

откуда

(3.10)

Итак, хотя функция п(v) пока нам неизвестна, мы уже знаем (см. предыдущий раздел), что интеграл от нее, взятый по всем возможным скоростям, равен 1. Это условие называют условием нормировки функции распределения. Функция распределения для газов была найдена теоретически Максвеллом (1859) и носит его имя. Далее мы установим ее вид.

Распределение Максвелла. Поскольку все направления движения молекул в пространстве равноправны, распределение скоростей должно быть изотропным и функция распределения n( v ) не может зависеть от направления скорости. Это означает, что n( v ) не может быть произвольной функцией от компонент скорости v_х, v_y, v_z, а должна зависеть лишь от абсолютной величины скорости

В зависимости от выбранной системы координат вероятность dN/N имеет различный вид.

В декартовой системе

(3.11)

В цилиндрической системе

(3.12)

В сферической системе

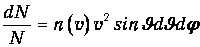
(3.13)

Далее предлагается простой, хотя и не вполне строгий вывод вида функции распределения. Рассмотрим процесс столкновения двух частиц, движущихся со скоростями v ₁ и v ₂. Пусть в результате соударения скорости молекул изменяются и превращаются в v ₃ и v ₄. Число таких столкновений в единицу времени в единице объема газа должно быть пропорционально числу молекул со скоростями вблизи v ₁ и v ₂, то есть произведению n(v₁) · n(v₂). Рассмотрим далее процесс соударения, являющийся обратным данному. При этом скорости молекул изменяются от значений v ₃ и v ₄ до значений v ₁ и v ₂. Число таких соударений в единицу времени в объеме пропорционально количеству молекул со скоростями вблизи v ₃ и v ₄, то есть n(v₃) · n(v₄).

В силу предположения о молекулярном хаосе и предположения о том, что число молекул с данными значениями скорости не изменяется процессами молекулярных столкновений в газе, находящемся в стационарном состоянии, можно считать, что число молекул, у которых скорости изменяются от значений v ₁ и v ₂ до значений v ₃ и v ₄, равно числу молекул, у которых скорости изменяются от v ₃ и v ₄ до v ₁ и v ₂. Отсюда следует, что

(3.14)

Равенство (3.14) выражает баланс частиц, получающих и теряющих соответствующую скорость, причем в процессе таких упругих соударений энергия молекул сохраняется (т₀ - масса молекулы):

(3.15)

Равенства (3.10), (3.14) и (3.15) представляют совокупности условий, которым должна удовлетворять искомая функция распределения.

Используя (3.15), выразим v₄ через v₁, v₂, v₃:

(3.16)

Функциональные уравнения (3.14) и (3.16) легко превратить в простое дифференциальное уравнение. Взяв логарифм от (3.14), имеем

(3.17)

Продифференцируем (3.17) по аргументу v₁:

(3.18)

Аналогично

(3.19)

Учитывая выражение (3.16), находим

(3.20)

Подставляя (3.20) в правые части соотношений (3.18) и (3.19), приходим к равенству

(3.21)

При этом мы должны помнить, что это равенство справедливо при совершенно произвольных значениях v₁, v₂, которые являются независимыми переменными. Это значит, что равенство (3.21) должно иметь место при совершенно произвольных значениях скоростей, поэтому оно может быть выполнено только тогда, когда правая и левая части (3.21) равны некоторой постоянной (которую мы обозначим через (-a)):

(3.22)

где переменная v может принимать значения v₁, v₂ или любое иное. Разделяя переменные, записываем (3.22) в виде

(3.23)

Интегрируя (3.23), находим

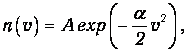
(3.24)

где А - постоянная интегрирования. Из физических соображений очевидно, что

Неограниченно большие скорости молекул маловероятны. Поэтому коэффициент a>0. Постоянная А определяется из условия нормировки (3.10):

(3.25)

Далее будет показано, что параметр a должен быть связан с абсолютной температурой T соотношением

(3.26)

С учетом (3.26) из (3.24) получим

(3.27)

Формула (3.27) и представляет собой искомое распределение молекул по скоростям.

Учитывая, что n(v) зависит только от модуля скорости, а их направления равновероятны, можно ввести функцию распределения f(v) молекул по абсолютной величине скорости. Для этого надо проинтегрировать выражение (3.13) по углам, что дает

(3.28)

Отсюда и из (3.27) следует выражение для функции распределения Максвелла f(v):

(3.29)

Величина f(v)dv есть вероятность найти частицу с модулем скорости, лежащим в интервале от v до v+dv. Условие нормировки распределения f(v) принимает теперь вид

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | Поиск по сайту: