 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение Клапейрона-Менделеева
ИДЕАЛЬНЫЙ ГАЗ
В нашем курсе мы постепенно продвигаемся от простого к сложному. До сих пор мы занимались в основном поведением одной частицы в разных силовых полях и свойствами этих полей. Но реальные физические системы состоят из невообразимо огромного числа частиц, так что проследить за движением каждой из них не под силу самым мощным компьютерам. Таким (макроскопическим) системам и посвящен в целом весь данный раздел.
В науке сложились два метода изучения свойств вещества и физических явлений, связанных с изменением свойств макроскопических тел: молекулярно-кинетический и термодинамический. Оба метода дополняют друг друга. В этом разделе мы сосредоточимся на молекулярно-кинетическом подходе.
Общие положения. Состояние системы. Температура
Молекулярно-кинетический подход. Молекулярная физика исходит из двух основных положений:
· любое тело - твердое, жидкое или газообразное - состоит из обособленных частиц, которые мы называем молекулами;
· молекулы всякого вещества находятся в беспорядочном хаотическом движении, не имеющем какого-либо преимущественного направления. Это движение называют тепловым, так как его интенсивность определяет температуру вещества.
Молекулярно-кинетическая теория ставит перед собой цель истолковать те свойства вещества, которые непосредственно наблюдаются на опыте (вязкость, теплопроводность и т. п.) как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением каждой отдельной молекулы, но лишь такими средними величинами, которые характеризуют движение и взаимодействие всей совокупности молекул. Молекулярно-кинетическая теория оперирует при этом основными закономерностями физики, действующими на микроскопическом уровне - законами классической механики, электродинамики и др. Поэтому она в состоянии предсказать величины многих физических параметров системы на основе, как говорят, первых принципов. В этой главе мы займемся выводом хорошо известных законов для идеальных газов на основе молекулярно-кинетической теории.
Состояние системы. В любом разделе физики изучение явлений начинается с выделения совокупности тел, которую называют системой.
| Система- это выделенная определенная совокупность физических тел. Окружающая среда- это все тела, которые не входят в систему, но могут влиять на ее свойства и поведение. |
Представим, например, газ (система) в закрытом цилиндре под поршнем (среда). Изменение положения поршня или температуры стенок цилиндра меняет состояние системы.
| Параметрысистемы - это величины, характеризующие состояние системы. |
Состояние таких простейших систем, как газ, характеризуется следующими макроскопическими параметрами: объемом V, давлением р, температурой Т. Естественно, нужны также параметры, определяющие систему - ее масса т, относительная молекулярная масса М (или масса моля m). Напомним, что
| Относительная молекулярная масса М - это безразмерная величина, равная отношению массы молекулы данного вещества к 1/12 массы атома углерода 12С. |
| Моль - это количество данного вещества, масса которого, выраженная в граммах, численно равна относительной молекулярной массе. |
| Масса моля (молярная масса m) имеет в СИ размерность кг/моль. |
При решении задач значения относительной молекулярной массы М элементов берутся из таблицы Менделеева. Молярная масса рассчитывается легко:
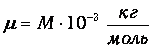
Например, для золота
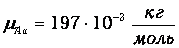
Для сложных веществ необходимо произвести простые арифметические действия, например

Вообще говоря, параметры системы могут иметь разные значения в различных ее точках. В этом случае системе в целом нельзя приписать определенных значений этих параметров, то есть имеет место неравновесное состояние. Опыт показывает, однако, что если внешние условия неизменны, то система с течением времени приходит в равновесное состояние: выравниваются давления и температуры ее отдельных частей, так что параметры системы принимают определенные значения, остающиеся постоянными сколь угодно долго. При этом внешние условия должны быть таковы, чтобы в системе не было переноса вещества, энергии, импульса и т. п.
В равновесном состоянии системы между параметрами имеется связь: заданные два параметра системы (например, ее температура и объем) однозначно определяют третий (в данном случае давление). Математически эту связь можно охарактеризовать уравнением состояния F(V, р, Т) = 0, где конкретный вид функции F зависит от свойств системы. Примером служат уравнения Клапейрона-Менделеева для идеального или Ван-дер-Ваальса для неидеального газов (эти уравнения будут рассмотрены далее).
Равновесное состояние может быть изображено графически точкой на плоскости (рис. 1.1), где по осям отложены какие-нибудь два из параметров - (р, V), (р, Т) или (V, T).

Рис.1.1. Равновесные состояния системы на диаграммах (р, V), (р, T) и (V, Т)
| Процесс - это всякий переход системы из одного состояния в другое. |
Процесс связан с нарушением равновесного состояния системы. Если состояние системы меняется со временем, то в системе происходит какой-то процесс. Обратное, вообще говоря, неверно: состояние системы может не меняться, хотя в ней и идет процесс. Например, при стационарном процессе переноса тепла состояние системы является неравновесным, хотя и остается неизменным в том смысле, что не меняются распределения температур по объему системы.
При бесконечно медленном протекании процесса можно считать, что в каждый данный момент времени состояние системы равновесно. Физически это означает, что характерное для процесса время tР много больше времени установления равновесия в системе te. Такой процесс называют равновесным процессом.
| Равновесный процесс- это бесконечно медленно протекающий процесс, при котором в каждый данный момент времени состояние системы равновесно. |
Равновесный процесс можно представить себе как последовательность равновесных состояний. В дальнейшем будут изучаться (если иное специально не оговорено) лишь равновесные процессы.
Поскольку состояние системы изображается точкой на диаграмме, а процесс -это последовательность равновесных состояний, то такой процесс изображается на диаграмме линией. Каждая точка на линии - условно равновесное промежуточное состояние системы. Равновесный процесс является процессом обратимым, то есть он может протекать в обратном направлении, проходя те же промежуточные состояния в обратном порядке, причем в окружающих телах не останется никаких изменений.
| Обратимый процесс- это процесс, который может протекать в обратном направлении, проходя те же промежуточные состояния в обратном порядке, причем в окружающих телах не останется никаких изменений. |
Естественно, что в системе тогда не должно действовать никаких сил, подобных силам трения. Ниже мы познакомимся с диаграммами, описывающими некоторые характерные процессы в термодинамических системах.
Зная состояние системы, мы можем найти различные функции состояния - физические характеристики, которые зависят только от состояния системы, то есть принимают те же значения всякий раз, когда система оказывается в данном состоянии независимо от ее предыстории.
| Функция состояния - это физическая характеристика, которая зависит только от состояния системы. |
Температура. Любая система обладает неким запасом внутренней энергии, не связанной с положением или движением системы как целого относительно внешней среды. О внутренней энергии мы еще поговорим подробнее, а сейчас нам достаточно интуитивного понимания, что, бросив с какой-то скоростью яйцо, мы его не сварим, хотя кинетическая энергия яйца и увеличится. Чтобы приготовить яйцо всмятку, его надо не бросить, а подогреть.
Для количественной характеристики внутренней энергии вводится понятие температуры. Температура занимает особое место в ряду физических величин. Опыт показывает, что она характеризует состояние теплового равновесия тел. Если привести в соприкосновение два тела с разными температурами, то в результате взаимодействия между молекулами эти тела будут обмениваться энергией. Через некоторое время температуры выровняются и передача теплоты прекратится, наступит состояние теплового равновесия. Состояние теплового равновесия и есть то состояние, в которое переходит с течением времени любая изолированная система.
Обычные способы определения температуры основаны на зависимости от нее ряда свойств тел (объема, давления и др.). При этом выбирается термометрическое тело и градуировка температурной шкалы. Наиболее распространенной является стоградусная шкала (шкала Цельсия). Участок этой шкалы между точками замерзания и кипения воды при нормальном атмосферном давлении делится на 100 равных частей. Такая часть называется градусом Цельсия (обозначается t ґC). Таким образом, точка кристаллизации воды соответствует 0 ґС, а точка кипения - 100 ґС. В США используют также шкалу Фаренгейта (обозначается t ґF). За нуль своей шкалы Фаренгейт выбрал наинизшую температуру, которую он мог воспроизвести в своей лаборатории - точку плавления смеси соли и льда. Точке замерзания воды в этой шкале соответствует температура 32 ґF, а точке кипения - 212 ґF. Этот интервал разделен не на сто, а на 180 частей (аналогично угловым градусам). Поэтому градус Фаренгейта меньше градуса Цельсия (фактор 100/180=5/9). Связь температур в этих двух шкалах дается формулами

В физике пользуются абсолютной шкалой температур Т (шкалой Кельвина), которая не зависит от термометрического тела, а устанавливается на основе законов термодинамики. Величина одного градуса в шкале Кельвина (обозначается К) совпадает с градусом Цельсия, а за нуль взята температура, при которой прекращается тепловое движение молекул. Связь абсолютной температуры Т с температурой по стоградусной шкале дается соотношением
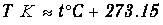
| (1.1) |
Таким образом, абсолютному нулю температуры Т=0 К в стоградусной шкале соответствует температура t=-273.15 ґС. Это значение было установлено опытным путем.
Примеры характерных температур в природе показаны на рис. 1.2.

Рис. 1.2. Температура различных физических процессов
Уравнение Клапейрона-Менделеева
В этом разделе мы знакомимся с уравнением состояния идеального газа.
| Идеальный газ - это настолько разреженный газ, что взаимодействием между его молекулами можно пренебречь. |
Эксперименты показали, что при обычных для нашего мира температурах и давлениях свойства реальных газов близки к свойствам идеального.
Поиск по сайту: