Броуновское движение

Задача о блуждающем матросе. Решим сначала классическую задачу о пьяном матросе. Матрос выходит из кабачка и собирается направиться домой. Он движется с постоянной скоростью v но в состоянии поддерживать выбранное направление движения лишь на пути l, то есть в течение времени

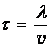
После этого его разворачивает, он теряет ориентировку и движется в каком-то другом направлении. Выбор направления каждый раз происходит случайным образом, так что любые направления равновероятны. Спрашивается, на каком среднем расстоянии R_KB от кабачка будет находиться матрос в момент времени t (предполагается, что t>>t). Слово «среднее» здесь означает следующее. Предположим, что такое происходит каждый день, и каждый раз мы измеряем удаление матроса от кабачка. Среднее квадратичное полученных значений при большом числе испытаний (скажем, за год) и дает нам искомую величину R_KB.

Итак, возьмем кабачок за начало отсчета координат и будем характеризовать положение матроса в момент времени радиус-вектором R. Путь матроса состоит из ломаных линий, число которых k=t/t. Пусть i - номер линии (i=1, 2,..., k). Перемещение матроса по линии с номером i задаем вектором r _i, так что для всех значений i имеем (рис. 4.8)

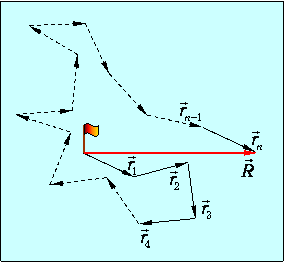
Рис. 4.8. Траектория блуждающего матроса

Тогда радиус-вектор R представляется в виде суммы векторов r _i

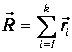
(4.34)

Возведем в квадрат обе части равенства (4.34):

(4.35)

Здесь q_ij - угол между векторами r _i и r _j. Усредним теперь обе части равенства (4.35) по всем случаям похода матроса в кабачок. Средние значения всех косинусов равны нулю в силу равновероятности выбора матросом следующего направления движения после прямого отрезка. Получаем тогда

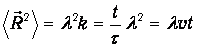
(4.36)

Отсюда следует искомое среднеквадратичное расстояние

(4.37)

Заметим, что это расстояние зависит от квадратного корня из времени в отличие от случая прямолинейного и равномерного движения. Это существенно меняет характер движения. Приведем численный пример. Пусть матрос движется медленно, со скоростью v=0.9 км/ч=0.25 м/ с. За время t=3 ч=10 800 с при прямолинейном движении он удалился бы на расстояние 0.9 · 3=2.7 км. Предположим, что по прямой он в состоянии двигаться только l=10 м. Тогда среднее его удаление от кабачка за то же время составит

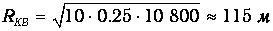
Броуновское движение и диффузия. Оставив нашего матроса петлять в окрестностях кабачка, мы вправе задать вопрос: а какое он имеет отношение к молекулярно-кинетической теории? Оказывается, самое прямое. Пусть в воде плавает пылинка, за которой мы наблюдаем в микроскоп. Пылинка подвергается ударам со стороны молекул среды, случайным образом меняя свое направление движения и скорость.

Случайность траектории пылинки здесь связана с тем, что:

· с разных сторон ее может ударить различное число молекул

· молекулы, ударяющие с одной стороны, могут в этот момент иметь большие скорости, нежели молекулы, ударяющие с другой.

Поэтому пылинка движется по ломаной траектории. Это явление называется броуновским движением. С повышением температуры интенсивность броуновского движения растет. При увеличении размеров пылинки случайности ее столкновения с молекулами сглаживаются, и броуновское движение становится ненаблюдаемым. Броуновское движение является самым непосредственным доказательством хаотического движения молекул. Наш блуждающий матрос - имитация броуновского движения. На этой простой задаче мы продемонстрировали характерную особенность - зависимость среднеквадратичного смещения пылинки от корня из времени движения. Произведение lv в уравнении (4.43) имеет ту же размерность и ту же структуру, что и коэффициент диффузии. Поэтому для броуновского движения также следует ожидать зависимости среднеквадратичного смещения вида

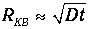
Броуновское движение тесно связано с диффузией. Обратимся ко второму закону Фика (4.9). Это уравнение первого порядка по времени, и оно позволяет найти функцию n(z, t), если задана начальная концентрация числа частиц n(z, 0). Мы не будем решать эту задачу точно. Отметим только, что с течением времени начальное распределение «расплывается» в пространстве и при этом изменяет свою форму. Но есть один вид распределения - гауссово, или нормальное распределение, - форма которого со временем остается неизменной (оно лишь «расплывается»). Мы займемся только этим, самым простым, случаем, позволяющим тем не менее получить все характерные особенности процесса. Для вычислений нам понадобятся два стандартных интеграла:

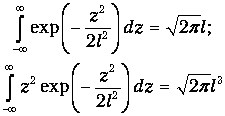
Пусть распределение концентрации частиц в начальный момент времени t=0 имеет вид

Вид этой функции представлен на рис.

Расплывание гауссова распределения концентрации частиц с течением времени: три кривые соответствуют трем различным значениям времени, измеренного в единицах t=l²(0)/(2D); по оси абсцисс отложены «безразмерные» расстояния, измеренные в единицах полуширины l(0) начального распределения; по оси ординат показано отношение концентрации частиц n(z, t) к ее максимальному значению n(0, 0) в начальный момент времени t=0; горизонтальные отрезки показывают среднеквадратичную ширину 2l(t)/l(0) каждого из распределений

Здесь N - полное число частиц, распределенных по оси z с концентрацией n(z, 0):

Величина l(0) характеризует ширину распределения. Действительно, выражение

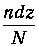
дает относительное число частиц на интервале (z, z+dz), то есть вероятность частице оказаться на этом отрезке. Поэтому среднее значение квадрата координаты равно

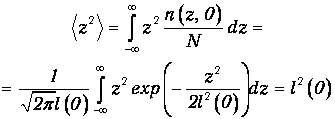
Если определить ширину распределения как расстояние между точками

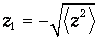
и

то

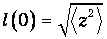
есть среднеквадратичная полуширина распределения в начальный момент времени t=0.

Как уже было сказано, гауссово распределение - единственное, не меняющее своей формы при расплывании. Это значит, что в произвольный момент времени t распределение будет иметь вид

(1)

Соответственно, для произвольного момента времени

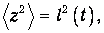
где пока неизвестная функция l(t) есть меняющаяся полуширина распределения.

Наша задача упростилась: вместо решения дифференциального уравнения в частных производных (4.9), нам достаточно теперь подставить туда (1), убедиться, что оно действительно является решением, и найти зависимость полуширины распределения от времени, то есть определить функцию l(t).

Продифференцируем (1) по координате z:

Продифференцируем (1) по z еще раз, принимая во внимание результат первого дифференцирования:

(2)

Теперь продифференцируем (1) по времени:

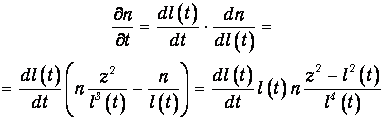
(3)

Подставляя выражения (2) и (3) в уравнение (4.9) второго закона Фика, убеждаемся, что n(z, t) в форме (4.46) действительно является его решением, если полуширина распределения l(t) удовлетворяет уравнению

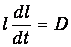
Это уравнение легко интегрируется:

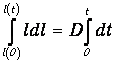
или

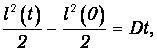
откуда находим зависимость полуширины распределения от времени:

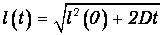
Если в начальный момент времени t=0 все молекулы были сосредоточены в одном месте (l(0)=0), то

что на новом уровне воспроизводит результат, угаданный нами при анализе блужданий матроса. Увеличение полуширины распределения дает смещение броуновской частицы. Выражение для среднеквадратичного смещения броуновской частицы
- это классический результат Эйнштейна-Смолуховского, построивших теорию броуновского движения.

Поиск по сайту: