О закономерностях в мире хаоса

Пусть имеется некоторый замкнутый сосуд небольшого (чтобы пренебречь действием внешних силовых полей) объема, заполненный газом. Предположим, что в газе установилось состояние равновесия.

Внешние условия должны быть такими, чтобы в системе не было переноса вещества, энергии, импульса и т. п.

Опыт показывает, что при равновесии:

· молекулы газа распределяются по всему объему замкнутого сосуда с равномерной плотностью

(3.1)

· молекулы газа обладают скоростями, равномерно распределенными по всем направлениям в пространстве.

Это означает, что число молекул, движущихся по любому направлению, должно быть одинаковым. Если бы это было не так и существовало бы направление преимущественного движения молекул, то в этом направлении возник бы поток газа. Из соображений симметрии очевидно, что в газе, заключенном в замкнутый сосуд и не подвергающемся воздействию извне, возникновение установившегося потока частиц невозможно, что подтверждается на опыте.

В пределах любым образом ориентированных, но одинаковых по величине телесных углов лежат направления движения в среднем одинакового числа молекул (рис. 3.1).

Рис. 3.1. Распределение молекул по направлениям движения

Соударения молекул не изменяют эту ситуацию. Для простоты мы будем рассматривать идеальный газ. С точки зрения кинетической теории, идеальный газ - простейшая молекулярно-кинетическая модель газа.

Модель идеального газа, как отмечалось ранее, предполагает следующие два свойства:

· силы взаимодействия между молекулами на расстоянии отсутствуют (взаимодействие возникает лишь при соударении молекул друг с другом или со стенками сосуда, причем соударения носят упругий характер);

· собственным объемом молекул можно пренебречь по сравнению с объемом, занятым газом.

Реальные газы близки к идеальному газу при малых плотностях. При уменьшении плотности средние расстояния между молекулами значительно превосходят линейные размеры молекул, и сила взаимодействия друг с другом уменьшается практически до нуля.

Функция распределения. Что такое распределение? Начнем с простого примера, позволяющего сформулировать необходимые определения. Пусть в некотором коллективе из 100 человек 10 имеют рост от 160 до 165 см, 25 - от 165 до 170, 35 - от 170 до 175, 15 - от 175 до 180, 10 - от 180 до 185 и остальные 5 - от 185 до 190. Это перечисление удобно изобразить в виде простой общепринятой диаграммы, рисуя вертикальные прямоугольники с высотой, пропорциональной числу людей данного роста (рис. 3.2). Такую диаграмму называют гистограммой. Если построить ее не для ста человек, а для взрослого населения целой страны, то можно ввести гораздо более мелкие подразделения по росту. Например, определять рост с точностью не 5 см, а 0.5 см (применительно к росту человека большая точность вряд ли имеет смысл).

Рис. 3.2. Гистограмма, изображающая распределение людей по росту, и примерный вид соответствующей функции распределения (штриховая кривая)

Допустим, однако, что некоторая изучаемая величина может задаваться сколь угодно точно, так что для весьма большого коллектива законно перейти от гистограммы к плавной функции распределения, график которой проходит через середины верхних сторон вертикальных прямоугольников гистограммы (штриховая кривая на рис. 3.2). Кривую такого рода мы и должны построить для распределения молекул газа по скоростям.

Случайные события. Раздел математики, изучающий случайные явления, называется теорией вероятностей. Ее основой является понятие случайного события как одного из возможных исходов некоторого испытания - процесса, который принципиально может воспроизводиться неограниченное число раз. На интуитивном уровне это понятие ясно, и мы не станем вдаваться в его формальное определение, принятое в современной математике. Выпадение числа 6 (или любого другого) при бросании игральной кости, появление красного или черного в игре в рулетку - примеры случайных событий.

Зачастую, однако, мы имеем дело с невоспроизводимыми событиями, к которым все же применима теория вероятности. Речь идет о количественных характеристиках массовых явлений. Скажем, на предприятии изготавливается транзистор. Он может быть дефектным или исправным, но в отличие от бросания игральной кости повторить процесс, изготовить тот же самый транзистор во второй, третий,..., миллионный раз уже невозможно. К этому же классу явлений относится появление данного числа вызовов на телефонной станции, возраст человека, занимающего определенное место на стотысячном стадионе, и т. п.

Можно ли случайные события или массовые явления описывать математическими формулами? Можно ли в мире случайностей найти некоторые закономерности? Такие попытки предпринимались издавна из-за потребностей практики. Еще в древних государствах делались прогнозы роста народонаселения и количества собираемого урожая и податей. Развитие страхового дела в средние века потребовало оценки степени опасности кораблекрушения. В XVII в. в Италии было основано первое общество по страхованию жизни, и его основателю надо было знать степень риска смерти клиента в зависимости от его возраста и профессии. Последним толчком к появлению теории вероятностей как самостоятельной математической дисциплины стало распространение азартных игр.

Вероятность случайного события. Каждому случайному событию можно приписать число, которое называется вероятностью события. Вероятность некоторого случайного события определяется относительной частотой его появления в ряду других случайных событий. Чем чаще происходит событие, тем больше его вероятность.

Пусть производится некоторое испытание, исходом которого является какой-то набор случайных событий А, В, С,.... Скажем, бросается игральная кость, которая предполагается геометрически правильной, так что все ее грани равноправны. Возможно всего шесть событий - выпадение чисел 1, 2,..., 6. Пусть произведено п испытаний, и событие А наступило k_n(А) раз. Величина

представляет собой относительную частоту события А в данной серии испытаний. Вообще говоря, значение P_n(А) колеблется при переходе от одной серии испытаний к другой. Если при увеличении числа п испытаний в серии число P_n(А) стремится к определенному пределу

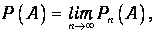
то этот предел Р(А) называется вероятностью события А. Если кость бросается достаточно много раз в нашем примере, то частота выпадения каждого из чисел будет одинаковой. Мы скажем, что вероятность выпадения любого из них равна 1/6.

Из классического определения вероятности следует, что она всегда заключена между нулем и единицей:

Обратные утверждения, вообще говоря, неверны. Например, не следует думать, что никогда не может осуществиться событие, вероятность которого равна нулю. События, которые осуществляются при бросании кости, дискретны: возможно выпадение единицы или двойки, но не двух с половиной. Но что делать, если события будут непрерывными? Например, вернемся к примеру группы людей. Какова вероятность того, что рост наудачу выбранного индивидуума будет в точности равен 176.543... см? Ясно, что эта вероятность равна нулю: существует бесчисленное множество непрерывно распределенных значений роста (возможных исходов измерений), так что знаменатель нашего определения вероятности бесконечно велик. Но все же может случиться так, что какой-то индивидуум имеет в точности такой рост. Чтобы избежать подобных трудностей, в таких случаях вместо вероятности события удобнее пользоваться плотностью вероятности, или, что то же самое, функцией распределения. Зная эту функцию, мы сможем, например, ответить на такой вопрос: какова вероятность того, что рост этого индивидуума заключен между 175 см и 180 см? В нашем примере эта вероятность составляет

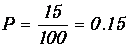
Та плавная кривая, которая соответствует гистограмме на рис. 3.2, при уменьшении интервала измерений роста приближается как раз к плотности вероятности.

Поиск по сайту: