 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Внутреннеобратимая тепловая машина
Помимо цикла Карно и технических циклов, используемых в различных двигателях, представляет интерес так называемая внутреннеобратимая тепловая машина (смысл названия станет ясен позже). Дело в том, что максимальный КПД, соответствующий циклу Карно, никогда не достигается на практике. Более того, если бы это было даже возможно, далеко не очевидно, что такую машину стоило бы создавать. Помимо КПД в реальной жизни немаловажную роль играют также простота устройства и управления, стоимость установки, ее надежность, скорость работы и тому подобные требования, которые зачастую конфликтуют между собой. В цикле Карно контакты рабочего тела с тепловыми резервуарами происходят при одинаковой температуре. Это значит, что тепло перетекает бесконечно медленно, что, конечно, очень непрактично. Представление о реальной производительности используемых установок можно получить, рассматривая внутреннеобратимую тепловую машину.
Предположим снова, что мы имеем два тепловых резервуара при температурах Ттaх и Tmin. Предположим также, что работа производится циклом Карно, функционирующим при температурах нагревателя T1 и холодильника Т2. Имеется в виду, что выполняется следующая цепочка неравенств: T mах> T1 > Т2 > Tmin. Иными словами, мы рассматриваем необратимый в целом процесс, внутри которого есть обратимый цикл. Тепло подается к рабочему телу при постоянной разности температур Ттах-T1 и отводится от него при постоянной разности температур Т2-Ттin (см. схему на рис.).
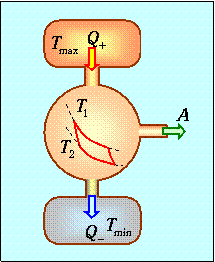
Цикл внутреннеобратимой тепловой машины, имитирующий реальные энергетические установки
В этом и заключается главное отличие от стандартного идеального цикла Карно, где соответствующие разности температур равны нулю.
корость теплообмена между рабочим телом и тепловыми резервуарами пропорциональна разности температур между ними:

| (1) |
где Q+, t+ - получаемое количество теплоты и время его передачи рабочему телу при контакте с нагревателем, a Q -, t - - количество теплоты, отдаваемой холодильнику, и время этого процесса. Величины с+ и с - - соответствующие коэффициенты теплопередачи. Тогда полное время t теплообмена равно

| (2) |
Время, затрачиваемое машиной на внутренний цикл Карно, определяется временем установления равновесия в рабочем теле, которое существенно меньше, чем время передачи тепла t. Поэтому t можно считать временем совершения полного цикла.
Как обычно, мы предполагаем, что отсутствуют потери тепла на трение и тому подобные процессы. Количества теплоты Q+ и Q-, а также совершенная работа А связаны между собой соотношениями, найденными нами при изучении цикла Карно:
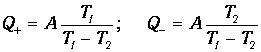
| (3) |
Подставляя (3) в (2), находим для времени осуществления цикла выражение

| (4) |
Мощность рассматриваемой машины равна A/t. Представим себе, что мы проектируем такую машину. У нас имеется возможность выбрать оптимальным образом температуры Т1, Т2, при которых функционирует внутренний цикл Карно. Выбирая их равными Ттах и Ттin соответственно, мы добьемся максимального КПД. Но из формулы (4) следует, что при этом

и выходная мощность машины стремится к нулю. Более практично выбрать температуры таким образом, чтобы максимума достигла выходная мощность. Приравнивая нулю производные по Т1 и Т2 от выражения (4) для t/A, находим уравнения для этих температур. Опуская детали, приведем лишь конечный результат: максимальная выходная мощность при этих условиях равна

| (5) |
Достигается это значение при температурах внутреннего цикла Карно

| (6) |
где параметр Т0, имеющий смысл некой средней температуры системы, определен соотношением
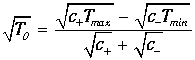
| (7) |
Очевидно, что КПД нашей машины равен КПД внутреннего цикла Карно
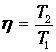
Поскольку отношение температур внутреннего цикла равно квадратному корню из отношения температур нагревателя и холодильника, находим КПД внутреннеобратимой машины:

| (8) |
Легко убедиться, что КПД меньше максимально возможного
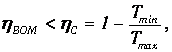
но зато мы выиграли в выходной мощности. Любопытно, что КПД оптимизированной по мощности внутреннеобратимой машины не зависит от коэффициентов с+ и с-: как и в цикле Карно, он определяется лишь отношением температур нагревателя и холодильника. Авторы концепции внутреннеобратимой машины (F. L. Curzon and В. Ahlborn, Amer. J. Phys. 43, 22, 1975) приводят следующую таблицу, где сравниваются несколько крупных электростанций. Видно, что формула (8) гораздо лучше соответствует практике, нежели КПД идеального цикла Карно.
Таблица
Сравнение наблюдаемых КПД нескольких электростанций разных типов с КПД цикла Карно hС и цикла внутреннеобратимой машины hВОМ
| Местонахождение и тип электростанции | Тmin, °С | Tmax, °С | hС | hВОМ | Наблюдаемый КПД |
| West Thurrock, Великобритания (уголная) | 0.64 | 0.40 | 0.36 | ||
| CANDU, Канада (ядерная) | 0.48 | 0.28 | 0.30 | ||
| Larderello, Италия (геотермальная) | 0.33 | 0.18 | 0.16 |
В заключение этого параграфа приведем численный пример.
Пример. Пусть коэффициенты теплопередачи с + одинаковы и таковы, что при разнице температур DТ=10 К мощность теплового потока между тепловыми резервуарами и рабочим телом составляет 1 кВт. Иными словами,

Пусть далее температуры резервуаров составляют Ттах=50ґС=823 К и Ттin=20ґС=293 К. Найдем максимальную выходную мощность внутреннеобратимой тепловой машины и температуры T1 и Т2, при которых должно функционировать рабочее тело, использующее цикл Карно.
Из формулы (5.29) следует, что при равенстве коэффициентов теплопроводности «средняя» температура Т0 определяется как

Используя соотношения (5.28), находим оптимальные температуры

КПД такой установки равен hBOM=0.403 (ср. hС=0.644). При таким образом выбранных температурах рабочего тела достигается максимальная выходная мощность, определяемая по формуле (5):
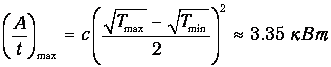
Поиск по сайту: