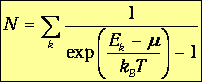Статистика Бозе-Эйнштейна

Рассмотрим теперь систему тождественных бозонов. В этом случае число n_i частиц в состоянии i может принимать любое значение от 0 до,бесконечности (или от 0 до N при фиксированном числе частиц). Рассмотрим какое-то конкретное состояние k системы с энергией Е_k. Тогда для вероятности, что в этом состоянии окажутся п частиц, получаем из основного соотношения (7.38)

(7.44)

где

Сумма W(n) по всем значениям п (включая и нулевое) равна вероятности того, что в состоянии k окажется какое-то количество частиц или не окажется ни одной. Очевидно, такая сумма должна быть равна единице:

(7.45)

Здесь мы использовали формулу

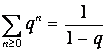
(7.46)

для суммы бесконечно убывающей геометрической прогрессии при

Теперь легко найти нормировочную постоянную:

(7.47)

и полное выражение для вероятности W(n). Нас интересует в первую очередь среднее число частиц в состоянии k, которое по смыслу вероятностей выражается как

Сумму ряда вида

нетрудно вычислить дифференцированием по q выражения (7.46):

(7.48)

Левая часть (7.48) может быть записана в виде

(7.49)

Вместе с (7.48) это приводит к результату:

(7.50)

Подставляя

находим

откуда следует основное соотношение квантовой статистики Бозе-Эйнштейна:

(7.51)

Разница по сравнению с соответствующей формулой (7.42) для фермионов имеется только в знаке перед единицей в знаменателе. Из-за этого нельзя теперь утверждать, что среднее число частиц в данном состоянии всегда меньше единицы: принцип Паули не распространяется на бозоны. По физическому смыслу все п_k > 0, следовательно, m<Е₀, где Е₀ - минимальная энергия системы (то есть энергия основного уровня). Для свободных частиц величина Е₀ равна нулю. Отсюда следует, что для свободных бозонов химический потенциал отрицателен. По-прежнему имеется уравнение связи m и N в случае фиксированного числа частиц:

(7.52)

При высоких температурах

то есть с ростом температуры число бозонов в каждом состоянии растет.

Если в системе число частиц не фиксировано, а определяется условиями равновесия (например, равновесие излучения с веществом, когда фотоны поглощаются и испускаются), то m=0. Применяя (7.51) к системе фотонов и учитывая, что для фотонов

приходим к формуле (7.15) и ее аналогу для фононов (7.30).

Заметим, что при

обе формулы (7.42) и (7.51) переходят в классическое распределение Больцмана. В этом случае

что можно интерпретировать как условие малой плотности частиц, то есть как квантовый аналог разреженного газа: в каждом квантовом состоянии фактически находится не более одной частицы. Значит, не существенно не только прямое взаимодействие частиц, но и их квантовое влияние друг на друга, обменные эффекты.

Поиск по сайту: