 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример. В аудиторию входит студентка
|
Читайте также: |
В аудиторию входит студентка. Оценим время, через которое запах ее духов достигнет экзаменатора, сидящего за столом.
Коэффициент диффузии молекул в газах мы оценили как

Расстояние l(t) до экзаменатора примем равным 4 м, а ширина начального распределения примерно равна диаметру головы студентки l(0)=0.2 м. Поскольку l(t)>>l(0), можно воспользоваться уравнением (4.52), откуда находим

Ответ явно несуразен и противоречит всему мировому опыту приема экзаменов. Из этого примера ясно, что распространение запахов по комнате происходит не вследствие диффузии, а из-за более быстрых процессов - конвекционных течений воздуха в комнате.
Численные оценки для броуновского движения. Если диффузионные процессы столь медленны, то как удалось наблюдать броуновское движение? Для ответа на этот вопрос мы оценим сейчас коэффициент диффузии пылинки в жидкости. Мы уже знаем, что среднеквадратичное смещение частицы вдоль какой-то оси линейно зависит от времени:

| (1) |
Этот закон можно использовать для определения коэффициента диффузии броуновских частиц. Рассмотрим теперь уравнение движения частицы вдоль выбранной оси z:

| (2) |
Здесь Fz - случайная сила, действующая на частицы со стороны молекул, а второй член в правой части - сила сопротивления движению частицы вследствие вязкости жидкости по закону Стокса (предполагается, что броуновские частицы являются шариками радиусом r). Поскольку нас интересует зависимость от времени квадрата координаты z, мы умножим уравнение (2) на z и используем соотношения

Усредняя получившееся уравнение, приходим к выражению
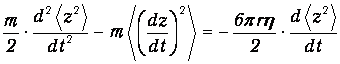
| (3) |
Здесь учтено, что <zFz>=0 из-за случайности сил, воздействующих на пылинку со стороны молекул. В силу (1)
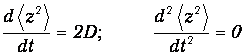
Подставляя эти значения в (3) и учитывая, что

находим искомое выражение для коэффициента диффузии броуновских частиц

Выполним теперь численные оценки. Радиус броуновских частиц (пылинок) r=0.5 · 10-6 м. Принимая h=10-3 Па · с (вода) и Т=300 К, получаем из (4)

что гораздо меньше коэффициента диффузии молекул духов студентки из рассмотренного выше примера. Тем не менее, броуновское движение наблюдаемо. Скажем, за 30 с среднеквадратичное смещение частицы составит

что в пять раз превышает диаметр пылинки. Поэтому такие смещения можно наблюдать в микроскоп. Пример демонстрирует извечную научную истину: сами по себе величины не могут априори считаться малыми или большими, все познается в сравнении.
Поиск по сайту: