Квантовая теория теплоемкости Эйнштейна

Квантовая теория устранила трудности, на которые натолкнулась классическая теория в вопросе теплоемкости твердых тел. Представим тело как систему N осцилляторов, не взаимодействующих друг с другом. Применим к этой системе закон распределения Больцмана, учитывая, что энергия гармонического осциллятора квантуется:

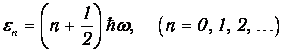
(7.3)

Если обозначить N_n число осцилляторов с квантовым числом n, причем

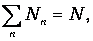
то средняя энергия, приходящаяся на одну молекулу в состоянии термодинамического равновесия, определяется выражением

(7.4)

Согласно распределению Больцмана, вероятность Р_п найти осциллятор в состоянии с квантовым числом п равна

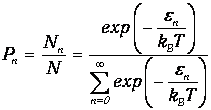
(7.5)

Подставляя соотношения (7.5) и (7.3) для Р_п и e_п в формулу (7.4) и выполняя суммирование, приходим к выражению для средней энергии гармонического осциллятора:

(7.6)

Формула (7.6) отличается от полученного ранее выражения наличием дополнительного первого слагаемого.

Это слагаемое

есть энергия «нулевых колебаний» гармонического осциллятора, которая не зависит от температуры и потому не вносит вклада в теплоемкость системы.

Выражение (7.6) было положено Эйнштейном в основу квантовой теории теплоемкости твердых тел. Эйнштейн отождествил кристаллическую решетку из N молекул с системой 3n_aN независимых гармонических осцилляторов с одинаковой собственной частотой w. Тогда внутренняя энергия одного моля определяется выражением

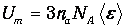
Дифференцируя его по температуре, получаем молярную теплоемкость кристаллической решетки твердых тел

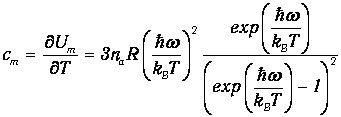
(7.7)

Это и есть формула Эйнштейна для теплоемкости кристаллов. При высоких температурах, когда

она переходит в классическую формулу

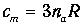
В другом предельном случае низких температур, когда

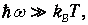
можно пренебречь единицей в знаменателе и получить

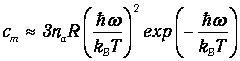
(7.8)

При Т, стремящемся к 0, полученное выражение стремится к нулю, как это требует тепловая теорема Нернста (см. разд. 5.7).

Поясним физический смысл этого результата. Из-за квантовой дискретности между основным и возбужденным уровнями системы осцилляторов имеется конечный энергетический зазор hw (энергетическая щель). Меньшее количество энергии осциллятор воспринять просто не в состоянии. При нулевой температуре в системе нет возбуждений - все осцилляторы находятся в основном состоянии. При небольшом повышении температуры тепловой энергии не хватает на преодоление этой щели, и лишь малое количество осцилляторов, пропорциональное

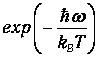
согласно закону Больцмана переходит на первый возбужденный уровень. Именно они ответственны за поглощение тепловой энергии и, соответственно, за малую теплоемкость кристалла при низких температурах. При высоких температурах тепловой энергии хватает на возбуждение многих вышележащих колебательных уровней, так что дискретность энергии уже не играет особой роли - мы возвращаемся к классическому результату Дюлонга и Пти.

Однако согласие с опытом теории Эйнштейна имеет только качественный характер. В выражении для с_т при низких температурах экспоненциальный множитель убывает быстрее, чем растет множитель 1/Т². Поэтому при приближении к абсолютному нулю с_т стремится к нулю практически по экспоненциальному закону. Опыт же показывает, что теплоемкость кристаллов изменяется при низких температурах не экспоненциально, а по закону

Как оказалось, эти расхождения теории Эйнштейна с опытом связаны не с существом квантовой теории, а с упрощением расчета, в котором предполагалось, что все гармонические осцилляторы колеблются с одной и той же частотой. На самом деле кристаллическую решетку следует рассматривать как связанную систему взаимодействующих частиц. При вычислении теплоемкости тело действительно можно рассматривать как систему гармонических осцилляторов, но с различными частотами. Задача сводится к отысканию спектра частот.

Поиск по сайту: