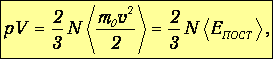Кинетическая теория идеальных газов

В этом разделе мы переходим к молекулярно-кинетическому описанию идеального газа.

При выводе основного уравнения молекулярно-кинетической теории газов будем считать молекулы маленькими твердыми шариками, упруго отражающимися от стенок сосуда. Силы взаимодействия возникают только при соударении молекул друг с другом или со стенками сосуда. Припишем каждой молекуле номер i (i=1, 2,..., N), где N - полное число молекул в системе.

Пусть молекула i подлетает к стенке, ограничивающей движение вдоль оси х, со скоростью v_ix и импульсом p_ix. При отражении молекулы от стенки знак ее импульса меняется на противоположный - p_ix, так что изменение х -компоненты импульса молекулы равно

Молекула после отражения долетит до противоположной стенки, снова отразится и в следующий раз подлетит к той же стенке через время

где l - длина сосуда. Поскольку импульс Dp_ix передается стенке каждые Dt секунд, на стенку со стороны одной молекулы действует средняя сила

(1.7)

(Заметим на будущее, что средние значения величин мы будем обозначать угловыми скобками).

Если в сосуде заключено N молекул, то полная сила F получится суммированием выражения (1.8) по всем молекулам:

При этом сумма произведений импульсов на скорости представима в виде

Так как все направления равноправны и молекулы совершенно одинаково отражаются от всех стенок сосуда, имеем

С другой стороны, среднее значение произведения импульса молекулы на ее скорость определяется как

Поэтому

и выражение для полной силы, действующей на стенку со стороны газа, приобретает вид

(1.8)

Разделив полную силу на площадь стенки S, мы получим выражение для давления газа р, где заменим произведение Sl на объем V сосуда. В итоге приходим к уравнению

(1.9)

Используем теперь тот факт, что скорость движения молекул при обычных для нашего мира температурах много меньше скорости света, так что импульс молекулы представим в виде р=m₀v, где т₀ - масса молекулы. Получаем тогда из (1.9) соотношения, которые называют основным уравнением молекулярно-кинетической теории газов:

(1.10)

или

(1.11)

Здесь п - концентрация молекул, <Е_ПОСТ> - средняя кинетическая энергия поступательного движения, приходящаяся на одну молекулу. Произведение N<Е_ПОСТ> есть полная кинетическая энергия поступательного движения всех молекул газа в данном объеме V.

Быть может, на первый взгляд трудно узнать в соотношениях (1.10-1.11) сходство со знакомым нам уравнением Клапейрона-Менделеева

поэтому слегка преобразуем последнее. Введем новую величину - постоянную Больцмана

Важность этой физической постоянной определяется тем, что с ее помощью устанавливается связь между энергией и температурой, как это видно уже по ее размерности. Далее используем, что

- число молей вещества в системе, а N_A - число молекул в одном моле, так что nN_A равно полному числу частиц в системе. Приходим тогда к следующей форме уравнения Клапейрона-Менделеева:

(1.12)

Сравнивая (1.10) с (1.12), мы видим, что, в сущности, имеем дело с аналогичным уравнением, если определить абсолютную температуру соотношением

(1.13)

Именно так абсолютная температура появляется в физике. Слева в уравнении (1.13) стоит средняя кинетическая энергия поступательного движения молекул газа. При нулевой температуре, как мы теперь воочию убеждаемся, действительно прекращается тепловое движение молекул, и потому абсолютный нуль недостижим.

Поиск по сайту: