Свидание в лесу, ежик в тумане и атомная бомба

Идея длины свободного пробега может быть использована для оценки видимости в лесу, в тумане или даже для грубой оценки критической массы урана в атомной бомбе.

Представьте себе, что у вас назначено свидание в лесу. С какого максимального расстояния R вы заметите своего партнера (а партнер - вас)? Положим, вы включаете фонарик, чтобы подать ему/ей сигнал. Если не учитывать рассеяние света, то все деревья отбрасывают тени, линейный размер которых можно считать примерно равным диаметру d деревьев. На рис. ваше место нахождения отмечено красным кружком, вокруг проведена окружность радиусом R, деревья показаны зелеными кружками, а их тени на окружности отмечены оранжевыми дугами.

Оценка максимального расстояния R видимости в лесу

Определим, какую часть окружности покрывают тени. Пусть п плотность посадки деревьев (их число на единицу площади). Если l среднее расстояние между деревьями, то

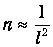
Внутрь окружности попадает pR²n деревьев. Полная длина тени на окружности равна поэтому pR²nd. Мы видим, что полная длина тени растет как квадрат радиуса и при каком-то значении R превысит длину окружности 2pR. Но если вся окружность покрыта тенями, то свет дальше не пройдет. Это значение R и будет максимальным расстоянием видимости в лесу. Теперь понятно, что оно определяется из равенства

то есть мы получили оценку

Для численного примера можно взять значения, исходя из своего жизненного опыта. Скажем, свидание назначено среди березок со средним диаметром ствола d=0.25 м и средним расстоянием между деревьями l=10 м. Тогда находим R=800 м.

Установим теперь связь полученного результата с формулой для средней длины свободного пробега. У нас одна молекула (световой луч) не имеет размера (d₁=0), размер прочих молекул равен среднему диаметру ствола (d₂=d) и, наконец, молекулы (стволы) - покоятся, то есть надо отбросить множитель 1.41. Получаем в результате в применении к нашей задаче выражение

Таким образом, найденный нами радиус видимости

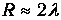
Вероятность свету преодолеть это расстояние без «столкновений» с деревьями равна

Иными словами, с вероятностью 86.5 % свет будет задержан деревьями.

Свидание в лесу происходило на плоскости. Сейчас мы вернемся в объемный мир. Тот же рисунок изображает теперь сферу радиусом R и препятствия в виде шариков диаметром d. Например, мы хотим оценить видимость для ежика, заблудившегося в тумане, и роль деревьев теперь исполняют водяные капли. Если концентрация капель равна п (их число в единице объема), то внутри сферы находится

Их тени на сфере представляют собой окружности площадью pd²/4. При максимальном расстоянии видимости тени покрывают всю сферу:

Отсюда находим расстояние видимости в тумане

Снова сравним этот результат с формулой (4.6) для длины свободного пробега молекулы в газовой среде, где надо отбросить фактор 1.41 и взять

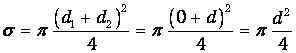
Получаем

Вероятность преодолеть путь R=3l без столкновений равна

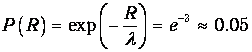
Стало быть, с вероятностью 95% столкновение на этом пути произойдет.

Получим численную оценку. Наши рассуждения годятся, если размер капель заметно (скажем, на один-два порядка) превышает длину световой волны. Так как видимый диапазон имеет длины волн 0.4 - 0.7 мкм, то для диаметра капель примем оценку d=10^{-4 м}. Для концентрации капель возьмем значение n=3 · 10⁷ м^-3 (о происхождении этого числа см. чуть ниже). Тогда видимость в тумане будет

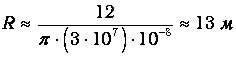
Концентрацию капель мы оценили следующим образом. Давление насыщенного водяного пара при, скажем, 20ґС (Т=293 К) равно р_Н=2.3 · 10³ Па. Применяя уравнение Клапейрона-Менделеева, находим плотность водяного пара при 100% влажности:

При резком понижении температуры весь пар конденсируется в капли указанного размера - образуется густой туман. Масса одной капли равна

Количество образовавшихся капель в объеме V находим как отношение массы пара m к массе капли m_КАП. Тогда концентрация капель определится из соотношения

При d=10^{-4 м} получаем использованное выше значение п=3 · 10^-7 м^-3.

Зависимость расстояния видимости в тумане от размера капель дается, таким образом, соотношением

При предельно малых капельках с диаметром порядка десяти длин световой волны d=10^-5 м видимость сокращается до одного метра. Что называется, «не видно дальше своего носа». При еще меньших размерах капель наша модель становится неверной, так как свет уже нельзя рассматривать просто как совокупность частиц с ничтожно малым размером. Начинают играть роль эффекты дифракции, и выражение для эффективного сечения взаимодействия света с каплями уже не будет определяться чисто геометрическим сечением капель.

Решенная задача имеет также отношение к вопросу о критической массе урана-235, применяемого для изготовления атомных бомб. Вместо света в этой задаче мы имеем нейтроны, а вместо капель - ядра ²³⁵U. При столкновении с ядрами нейтроны расщепляют их на осколки, и при этом вылетает еще 3 - 4 нейтрона. При критическом радиусе R_крит количество нейтронов не будет уменьшаться и возникнет самоподдерживающаяся цепная реакция - произойдет атомный взрыв. За основу определения критического радиуса можно взять радиус видимости

уменьшенный в k раз (k=3.5 - коэффициент размножения нейтронов). Поскольку

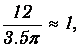
получаем

Радиус ядра

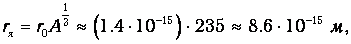
где r₀=1.4 · 10^{-15 м} - радиус ядра с массовым числом А=1, то есть протона (нейтрона). Поэтому эффективный диаметр взаимодействия равен

В справочнике (например, Российском энциклопедическом словаре) находим плотность урана r_U=19 · 10³ кг/м³. Массу ядра урана-235 определяем по массе протона

Отсюда находим концентрацию ядер

Теперь мы можем оценить критический радиус R_крит

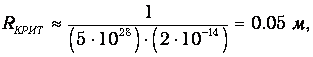
критический объем V_крит

и критическую массу М_крит

Отметим, что никаких секретов производства ядерного оружия мы не выдаем: слишком грубы эти оценки. Единственная наша цель - продемонстрировать еще раз единство законов физики, действующих в самых разнообразных системах.

Поиск по сайту: