Статистический смысл энтропии

Закон возрастания энтропии является иной формулировкой второго начала термодинамики. Как мы сейчас убедимся, его смысл сводится к тому, что система стремится к более вероятному состоянию. Вспомним задачу о смешивании газов с разными давлениями. Вообще говоря, можно представить себе обратный процесс: газ и сосуде самопроизвольно разделится на две части, так что давления в каждой из частей будут различаться. Никакой закон сохранения не противоречит такому процессу, но он никогда не происходит в реальности, поскольку вероятность его ничтожно мала. Закон возрастания энтропии связан с тем, что данное макроскопическое состояние системы (определяемое параметрами Т, р, V) может быть реализовано множеством способов при различных микроскопических состояниях (определяемыми положениями и скоростями молекул). Понятно ведь, что можно поменять импульсы пли положения какой-то пары молекул, и мы получим другое микроскопическое состояние, но термодинамически система не изменится. Число микроскопических состояний, соответствующих тому же макроскопическому состоянию, определяет вероятность последнего: чем большим числом способов можно его реализовать, тем оно вероятнее. Возрастание энтропии, как уже говорилось, означает лишь то, что система стремится перейти в более вероятное состояние, которое реализуется большим числом микроскопических состояний.

Чтобы убедиться, что энтропия действительно связана с вероятностью, рассмотрим еще один неравновесный процесс. Пусть имеется сосуд объемом V, разделенный на правую и левую половины непроницаемой перегородкой. Пусть идеальный газ из N молекул содержится в левой половине сосуда, в то время как правая половина от молекул свободна. Перегородку делают проницаемой, так что газ может адиабатно расширяться в пустоту, как в эффекте Джоуля-Томсона. Определим изменение энтропии газа. Поскольку при расширении в пустоту не совершается работы против внешней силы, а тепла извне не поступает в силу условия адиабатности, идеальный газ не изменяет свою температуру. Увеличение же в два раза объема, занимаемого молекулами газа, приводит к двукратному уменьшению его давления от начального значения р₁ до конечного р₂=р₁/2. Поэтому энтропии газа до и после расширения равны, соответственно:

(5.28)

а изменение энтропии дается выражением

(5.29)

Каково же происхождение фактора 2^N под знаком логарифма? Проследим за какой-нибудь молекулой. При непроницаемой перегородке она могла находиться только в левой половине сосуда, а потом ей стали доступны обе половины. Число способов размещения данной молекулы увеличилось в два раза, и так - для каждой из N молекул. Поэтому полное число способов размещения молекул увеличилось в 2^N раз. В такое же число раз вероятность состояния газа, равномерно занимающего полный объем сосуда, больше вероятности состояния, когда при проницаемой перегородке все молекулы сосредоточатся в левой половине, оставив правую свободной. Это не противоречит никаким законам, но при N=N_A=6.02 · 10²³ молекул (один моль вещества) вероятность такого события фантастически, грандиозно, невероятно мала (2^-NA).

Еще один пример на ту же тему. Возьмем тот же сосуд, и пусть в каждой из его половинок находится равное число N/2 молекул при одинаковых температуре и давлении. Мысленно пометим молекулы левой половины черным цветом, а правой - белым, и пусть молекулы слева и справа больше ничем не отличаются. После этого соединим сосуды и определим изменение энтропии DS. После перемешивания температуры газов не изменятся, а их парциальные давления уменьшатся в два раза, так что полное давление, равное сумме парциальных, останется прежним. Поэтому процесс перемешивания сродни расширению газов черных и белых молекул в пустоту, и мы можем воспользоваться результатом (5.29), учитывая, что число молекул каждого цвета равно теперь N/2. Складывая затем изменения энтропии обоих газов, получаем

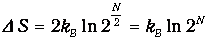
(5.30)

(N пробегает теперь только четные значения). Убедимся, что и в данном случае 2^N описывает увеличение числа способов распределения молекул по сосуду.

Рассмотрим рис. 5.4. Пусть у нас есть всего по одной молекуле в каждом из сосудов (N=2). Раньше желтая молекула могла находиться только в левом сосуде, а после смешивания для нее стали доступны обе части соединенного сосуда. Аналогично расширились возможности для голубой молекулы, которая ранее была ограничена в своих передвижениях правым сосудом.

Рис. 5.4. Возрастание энтропии при смешивании одинаковых порций газа: при подсчете различных способов распределения молекул по частям соединенного сосуда надо различать каждую желтую и каждую голубую молекулу, для чего они снабжены «хвостиками», торчащими налево либо направо

Итак, после смешивания молекулы свободно блуждают по сосудам и мы имеем в четыре (2²) раза больше вариантов их размещения (см. верхнюю часть рис. 5.4). Если у нас имеется N=4 молекулы, то после соединения у них появляется в 2⁴=16 больше возможностей распределиться но объему системы (нижняя часть рисунка). Ясно, что в общем случае N молекул число 2^N действительно есть не что иное, как фактор, в который возрастает число способов распределения молекул по объему системы.

Можно дать статистическое определение энтропии:

(5.31)

где W - число микроскопических способов, которыми можно реализовать данное макроскопическое состояние. Расчет вероятности макроскопических состояний и подстановка их в эту формулу приводит к прежним выражениям для энтропии идеального газа. Использование логарифма в определении энтропии позволяет свести умножение вероятностей к сложению энтропии. В наших примерах энтропия, приходящаяся на одну молекулу, возросла на величину

Двойка под логарифмом - это увеличение в два раза свободного пространства, доступного молекуле. Энтропия газа из N молекул в N раз больше:

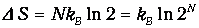
В классической статистике энтропия определяется с точностью до аддитивной постоянной S₀. В квантовой статистике, оперирующей дискретными уровнями энергии, эта постоянная может быть определена. Оттуда, в частности, следует теорема Нернста, иногда называемая третьим началом термодинамики:

Действительно, при абсолютном нуле температуры всякое тепловое движение прекращается и все молекулы находятся в состоянии с наинизшей энергией. Поэтому есть только один способ реализации такого состояния (W=1), так что S=0.

Представим себе, что мы снимаем фильм о смешивании молекул в сосудах. Сначала у нас слева - желтые молекулы, а справа - голубые. Молекулы сталкиваются, путешествуют по сосудам и в конечном итоге равномерно перемешиваются (так сказать, их смесь дает более или менее ровный зеленый цвет). Такое поведение системы большого числа частиц соответствует нашей практике. Запустим теперь фильм в обратном направлении. В каждом отдельном кадре, то есть в конкретном акте соударения молекул, мы не увидим ничего особенного. Законы механики не нарушатся на нашем экране, поскольку они обратимы. Но конечный итог «обратного» фильма поистине чудесен: казалось бы, беспорядочные столкновения молекул привели к разделению зеленого цвета на желтый слева и голубой справа. В таком процессе энтропия уменьшается, а система приходит от беспорядка к порядку. На самом деле каждая молекула имела в точности такие скорости и положения, испытывала именно такие, а не другие столкновения, чтобы в конце концов прийти в ту половину сосуда, где она оказалась. Такое событие в высшей степени невероятно, хотя и не противоречит микроскопическим законам физики. Закон возрастания энтропии утверждает, что система с течением времени имеет тенденцию перейти в менее упорядоченное состояние. Как говорится, «энтропия возрастает, а мир стремится к хаосу». Вопрос же о самоорганизации материи, о возникновении порядка из хаоса - предмет совсем другой науки, синергетики.

Поиск по сайту: