Вероятностный смысл энтропии

Глубокое понимание сущности энтропии невозможно без выяснения того, что же она представляет собой с точки зрения движения и взаимодействия молекул. Исследование этого вопроса было предпринято Л. Больцманом, главный результат которого заключается в короткой формуле, которую он завещал выбить на своем надгробии. В современных обозначениях она записывается следующим образом:

,

где S — энтропия системы молекул, k — коэффициент пропорциональности (по­сто­ян­ная Больцмана), W — статистический вес данного макроскопического состояния системы. Чем больше W, тем больше и тем больше энтропия S.

Статистический вес — это число способов, которым можно реализовать данное макроскопическое состояние системы.

Пояснить определение статистического веса можно на примере ящика с двумя одинаковыми отделениями, между которыми имеется перегородка с небольшим отверстием. Начнем заполнять ящик молекулами. Для определенности будем считать, что всего в нашем распоряжении молекул.

Способы, «ко­то­ры­ми можно реализовать данное состояние системы», отличаются друг от друга тем, какие именно молекулы попали в левое отделение. Представим, что все 10 молекул пронумерованы. Состояние 4|6 можно получить, поместив в левое отделение молекулы номер 1, 2, 3 и 4. А можно — 1, 3, 5, 7 или 7, 8, 9 и 10.

Наименьший статистический вес W = 1 имеют состояния 0|10 и 10|0, поскольку есть лишь один способ поместить все молекулы в правое (левое) отделения. Статистический вес состояния 1|9 равен 10 (по­сколь­ку одну молекулу, помещаемую в левое отделение, можно выбрать из всех имеющихся десятью способами). Если рассмотреть состояние с двумя молекулами в левом отсеке, то первую из них мы можем выбрать опять десятью способами, а вторую — девятью (одну из 9 оставшихся). Всего вариантов выбора получается 10×9 = 90, но это число надо разделить пополам во избежание двойного счета. Действительно, если мы выбираем для левого отделения сначала молекулу №5, а затем — №3, то это тот же способ размещения, что дает выбор сначала третьей, а потом уж пятой молекулы. Таким образом, статистический вес состояния 2|8 (и состояния 8|2) равен 45. Нетрудно догадаться, что максимальным статистическим весом обладает состояние, в котором молекул в отделениях поровну (рис. 4.8).

Поместим все десять молекул в левое отделение и закроем ящик. Молекулы беспорядочно двигаются, сталкиваются друг с другом и со стенками, время от времени проскакивая через отверстие из одного отделения в другое. Можно ли ожидать, что, открыв через некоторое время ящик, мы опять обнаружим все десять молекул в одном отделении? Здравый смысл и интуиция подсказывают, что вряд ли — скорее всего, мы увидим состояние 5|5. Физик вместо «скорее всего» предпочтет сказать: «ве­ро­ят­ность состояния 5|5 больше, чем вероятность состояния 0|10», поскольку вероятность есть величина, выражаемая числом. Но наиболее вероятное состояние 5|5 — это состояние с наибольшим статистическим весом, а значит, и энтропией. Таким образом, чем больше вероятность состояния, в котором находится система, тем больше ее энтропия.

Энтропия является мерой вероятности обнаружить систему в данном состоянии.

Отсюда еще одна формулировка закона возрастания энтропии:

с течением времени замкнутая система самопроизвольно переходит из менее вероятных в более вероятные состояния.

Выясненный вероятностный характер понятия энтропии обуславливает и вероятностный, статистический характер второго закона термодинамики. Конечно, состояние 5|5 более вероятно, чем состояние 0|10, но это не означает, что последнее невозможно. Есть примерно один шанс из тысячи, что, заглянув в очередной раз в ящик, мы обнаружим, что все молекулы опять собрались в правом отделении. Физик скажет, что возникла флуктуация.. Поэтому последнюю формулировку второго закона следует понимать как утверждение о наиболее вероятном, но не единственно возможном развитии событий, как утверждение об общей тенденции. Правда, чем больше число молекул в системе, тем жестче выдерживается эта тенденция. Общее правило гласит, что в системе N частиц реально можно наблюдать флуктуации относительной величины примерно 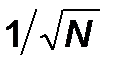. В макроскопических системах, для которых N ~ 10²⁴ и , сколько-нибудь значительные отклонения от среднего не наблюдаются никогда.

Поиск по сайту: