Векторное и смешанное произведение векторов. Свойства и геометрический смысл. Вычисление через координаты векторов

Векторное произведение

Векторное произведение векторов и - вектор, обозначаемый или для когорого:

1) ( - угол между векторами и , );

2)

3) тройка , , - правая.

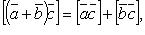
Свойства векторного произведения: если , то 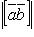равен площади параллелограмма, построенного на приведенных к общему началу векторах и .

Векторное произведение в координатах

Если , то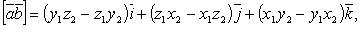

или

или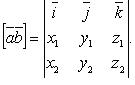

В частности

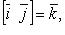
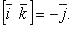
Некоторые соотношения

(двойное векторное произведение),

(тождество Якоби),

Смешанное произведение трех векторов

Определение: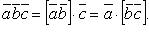

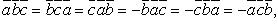
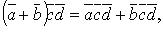
Свойства смешанного произведения: - компланарны.

Если V - объем параллелепипеда, построенного на приведенных к общему началу векторах , и , то если тройка правая, и если тройка левая.

Смешанное произведение в координатах

Если то

15. Простейшие задачи аналитической геометрии на плоскости. 1) Вычислим расстояние между двумя точками на плоскости:
2) Деление отрезков в данном отношении. Пусть на плоскости даны две точки с координатами М1(X1;Y1) и M2(X2;Y2). Найти координаты точки М лежащей между М1 и М2 на отрезке М1М2, если выполняется условие: 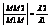. Проекции точки М на ось абсцисс будет делить отрезок X1X2 в той же самой проекции, потому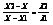 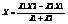, l1X2 - l1X = l2X - l2X1. Аналогичным образом можно получить, что , , ,

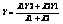16. Полярные координаты.
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, луча ОА, исходящего из этой точки, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными. Полярными координатами произвольной точки М (относительно заданной системы) называются числа r = ОМ и q < АОМ. Угол q при этом следует понимать так, как принято в тригонометрии. Число r называется первой координатой, или полярным радиусом, число q- второй координатой, или полярным углом точки М. Символ М (r;q) обозначает, что точка М имеет полярные координаты r и q. Полярный угол q имеет бесконечно много возможных значений. Значение полярного угла, удовлетворяющее неравенствам -p < q ≤ +p, называется главным. В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1) пользоваться одним и тем же масштабом, 2)при определении полярных углов считать положительными повороты в том направлении, в каком следует вращать положительную полуось абсцисс, чтобы кратчайшим путем совместить ее с положительной полуосью ординат. При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки к декартовым координатам той же точки осуществляется по формулам cosq, sinq. В этом же случае формулы , tgq = являются формулами перехода от декартовых координат к полярным. При одновременном рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштабов для обеих систем одинаковыми.

Поиск по сайту: