 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Бесконечно малые функции
Функция f (x) называется бесконечно малой функцией в точке х = х 0, если
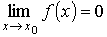
Аналогично определяются бесконечно малые функции при x → ∞, x → + ∞, x → – ∞, x → x 0 – 0, x → x 0 + 0.
Можно дать равносильное определение бесконечно малой функции «на языке ε – δ: функция f (x) называется бесконечно малой в точке х = х 0, если для любого как угодно малого ε > 0 существует δ = δ(ε) > 0, такое, что для всех х, удовлетворяющих неравенству 0 < | х – x 0 | < δ, выполняется неравенство | f (x) | < ε. Или в символьном виде
( ε > 0) (
ε > 0) (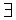 δ = δ(ε) > 0)(
δ = δ(ε) > 0)( 0 < | х – х 0| < δ): | f (x) | < ε.
0 < | х – х 0| < δ): | f (x) | < ε.
Имеет место следующая теорема: функция f (x) в окрестности точки х 0 отличается от своего предельного значения A на бесконечно малую функцию.
Доказательство. Пусть
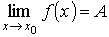
Рассмотрим разность f (x) – А = α(х). Так как
 ,
,
то функция α(х) является бесконечно малой при x → х 0.
Поиск по сайту: