Общая теория систем линейных уравнений. Понятие ранга матрицы. Теорема Кронекера-Капелли

Наивысший порядок не вырожденных миноров называют – рангом (rang(A))

Матрица, получающаяся конкатенацией матрицы и столбца правых частей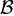

называется расширенной матрицей системы линейных уравнений.

Теорема [Кронекер, Капелли]. Система совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

При выполнении этого условия, система имеет единственное решение, если число неизвестных 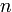совпадает с общим значением ранга , и бесконечное множество решений, если 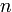меньше этого значения. Доказательство необходимости. Пусть существует решение системы, тогда

т.е. столбец 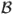линейно выражается через столбцы . Но тогда

Следовательно .

Доказательство достаточности проводится в следующем пункте.

Обозначение для ранга матрицы соответствует по смыслу этому же обозначению в методе Гаусса: после приведения к трапециевидному (или треугольному) виду в системе л.у. должно остаться ровно линейно независимых уравнений, явно содержащих неизвестные. Это утверждение вытекает из способа вычисления ранга матрицы по методу элементарных преобразований.

Пример. Исследовать совместность системы уравнений

в зависимости от значения параметра .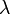

Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы . Если он отличен от нуля — система совместна.

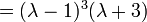. По теореме Крамера при и при решение системы единственно:

Осталось исследовать критические случаи: и 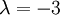: определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При имеем

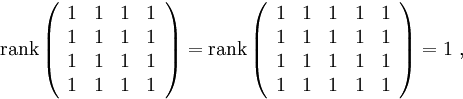
и система совместна. Она эквивалентна единственному уравнению

которое имеет бесконечно много решений.

При :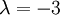

и система несовместна.

Наивысший порядок не вырожденных миноров называют – рангом (rang(A))

Ответ. Система несовместна при ; она имеет бесконечное множество решений

при и единственное решение при .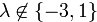

9. Векторные величины. Линейные операции с векторами.
Вектор – направленный отрезок, таким образом чтобы задать вектор необходимо задать его длину и направление.
Два вектора называют равными, если они имеют одинаковую длину и направление.
Вектор называют нулевым, если длна равна нулю (он не имеет направления).
Если на плоскости введена прямоугольная система координат, то для того чтобы задать вектор

надо указать начало вектора т. А и его окончание т. В., в этом случае вектор обозначается

Пусть т. А имеет координаты , т. В

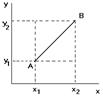
Тогда
Пусть a и b обозначают углы, которые образует вектор с положительным направлением координатных осей. a и b - углы определяющие направление вектора , cos этих углов называются направляющими:

,
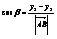
т.к. при параллельном переносе ни длина ни направление вектора не изменяется, то удобно расположить все векторы таким образом, чтобы они начинались в начале координат. В этом случае для задания вектора достаточно указать т., где он заканчивается.

Действия с векторами.

На основе полученных векторов, построим параллелограмм. Проведём диогональ АВ. Тогда Для каждого вектора АВ не равного нулевому существует противоположный, который такой же длины но другого направления. Вектор обратный вектору АВ, обозначается (-АВ)
Разностью двух векторов А₁В₁ и А₂В₂ называют вектор .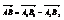
Вектор АВ называется произведением вектора А₁В₁ на вещественное число l и обозначается следующим образом:

а) если длина вектора АВ равна l и вектор АВ имеет тоже направление что и вектор А₁В₁.
б) если l=0, то l 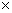А₁В₁=0
в) если l<0, то l 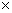А₁В₁=(-( ))

10. Линейная зависимость и независимость векторов. Коллинеарные и компланарные вектора.
Два вектора называются коллинеарными, если они лежат на одной прямой или на || прямых.

Если векторы и являются коллинеарными, то они наклонены под одним и тем же углом положительного направления оси ОХ, значит 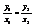Þ , Þ - условие коллинеарности векторов.
Два вектора называются компланарными если они находятся в разных плоскостях и не пересекаются.

11.Теорема о разложении произвольного вектора. Базис и координаты вектора.

12. Скалярное произведение векторов. Угол между векторами.

Скалярным произведением векторов a и b называют число равное произведению длин этих векторов на cos угла между ними. Пусть ça çи çb ça - угол между векторами, тогда из определения следует ab = ça ç× çb çcos a. Пусть a1 – угол который образует вектор a с положительным направлением оси ОХ. a2 – угол который образует вектор b с положительным направлением оси ОХ. a=a1-a2 ab = êaê×êbêcos (a1-a2).

êa êcos a1 × êb êcos a2 + êa êsin a1 × êb êsin a2 = x1x2+y1y2. Таким образам скалярное произведение векторов a и b можно вычислить как сумму произведения их соответствующих координат. Это определение скалярного произведения эквивалентно первоначальному. Свойства векторов: 1.)ab = ba. 2.)a × 0 = 0. 3.) a(b +c) = ab + ac. 4.) (la) × (lb) = l(ab). 5.) aa = êa ê². 6.) aa ³ 0 aa = 0 Û a = 0. 7.) ab = 0 Û a ^ b. Предполагается, что нулевой вектор ^ любому вектору. Аналогичным образом определяется скалярное произведение для векторов расположенных в трехмерном пространстве свойства 1 –7 остаются неизменными.

Поиск по сайту: