АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Применение дифференциала для приближенных вычислений значений функции

Читайте также:
  1. I. ПРИМЕНЕНИЕ ГЕОМЕТРИИ
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. Ms Excel: мастер функций. Логические функции.
  4. Абстрактные классы и чистые виртуальные функции. Виртуальные деструкторы. Дружественные функции. Дружественные классы.
  5. Алгебраическое интерполирование функции.
  6. Асимптоты графика функции.
  7. Банки и их функции. Банковская система
  8. Билет 35(Деньги; сущность и функции. Понятие и типы денежных систем. Денежные агрегаты. Закон денежного обращения.)
  9. Биосфера: понятие и современные представления, функции. Вклад Ж-Б Ламарка, Э. Зюсса, В.И. Вернадского. Эволюция биосферы. Границы биосферы.
  10. Булевы функции. Способы задания. Примеры.
  11. Бухгалтерський облік призначений,
  12. В условиях рынка прибыль субъектов торговли выполняет сле-дующие функции.

Пример 1. Дана функция z = x 2 + y 2 – 2· x + 2· y и две точки А(1, 2) и В(1,08; 1,94). Найти:

  1. значение функции в точке В;
  2. приближённое значение z 1 функции в точке В, заменяя приращение функции при переходе от точки А к точке В дифференциалом; оценить в процентах относительную погрешность вычисления при замене приращения функции дифференциалом.

Решение. Вычислим значение функции в точке В:

z (B) = 1,08² + 1,94² – 2·1,08 + 2·1,94 = 6,65.

Приближенное значение z 1 в точке В найдём по формуле линеаризации:

z 1(B) = z 0 + dz, где z 0 = z (1, 2) = 12 + 22 – 2·1 + 2·2 = 7.

Найдём приращения аргументов

Δ x = x – x 0 = 1,08 – 1 = 0,08; Δ y = y – y 0 = 1,94 - 2 = - 0,06.

Найдём значения частных производных функции в точке А

.

Найдём значение дифференциала

Приближённое значение функции в точке В равно z = 7 − 0,36 = 6,64.
Относительная погрешность вычисления равна

Пример 2. Гипотенуза с и катет а определяются с максимальными абсолютными погрешностями | Δ с | =0,2; |Δ а | = 0,4 и соответственно равны с = 75, а = 32. Определить угол А по формуле и максимальную абсолютную погрешность |Δ А| измерения этого угла.
Решение. Из условия примера имеем . Вычислим частные производные

.

Заменяя приращение величины её дифференциалом, получим

.

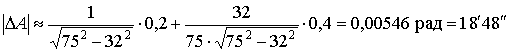Таким образом,

.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)