Раскрытие неопределенностей. Правило Лопиталя

1. Неопределенность вида 0/0. Первое правило Лопиталя.

Если 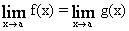= 0, то , когда последний существует.

2. Неопределенность вида ¥ / ¥. Второе правило Лопиталя.

Если 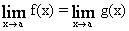= ¥, то , когда последний существует.

3. Неопределенности вида 0 × ¥, ¥ - ¥, 1 ^¥ и 0 ⁰ сводятся к неопределенностям 0/0 и ¥ / ¥ путем алгебраических преобразований.

Пример. Найти предел функции y = при x ® 0.

Решение. Имеем неопределенность вида ¥ - ¥. Сначала преобразуем ее к неопределенности вида 0/0, для чего достаточно привести дроби к общему знаменателю. К полученному выражению два раза применим правило Лопиталя. Записывая последовательно все промежуточные вычисления, будем иметь:

= = = =
= = .

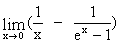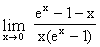50. Применение производных для исследования функций. Условия монотонности.
1. Область определения.
2. Особые свойства функции: чётность или нечётность, периодичность.
3. Корни, промежутки знакопостоянства.
4.

Непрерывность, характер точек разрыва (односторонние пределы), пределы на бесконечности.
5. Асимптоты.
6. Производная, исследование функции на монотонность и экстремумы.
7. Вторая производная, исследование функции на выпуклость и перегиб.
8.

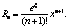
Нахождение значения функции и ее производной в характерных точках (пересечения с осями координат, экстремума, перегиба), нахождение нескольких дополнительных точек графика (не обязательно, используется для построения более точного графика).
9. Построение эскиза графика.
Исследование дифференцируемой функции на максимум и минимум с помощью первой производной:
1) Ищем первую производную функции, т. е. f’(x)

2) Находим критические значения аргумента x; для этого:
а) приравниваем первую производную к нулю и находим действительные корни полученного уравнения f’(x)=0;
б) находим значение x, при которых производная f’(x) терпит разрыв.
3) Исследуем знак производной слева и справа от критической точки. Так как знак производной остается постоянным в интервале между двумя критическими точками, то для исследования знака производной слева и справа, например, от критической точки x₂ достаточно определить знак производной в точках a и b (x₁<a<x₂, x₂<b<x₃, где x₁ и x₃ – ближайшие критические точки).
4) Вычисляем значение функции f(x) при каждом критическом значении аргумента.
Исследование функции на максимум и минимум с помощью второй производной:
1) Пусть при x=x₁ производная функции y=f(x) обращается в нуль, т.е. f’(x₁)=0. Пусть, кроме того, вторая производная f’’(x) существует и непрерывна в некоторой окрестности точки x₁. Тогда справедлива следующая теорема: Пусть f’(x₁)=0; тогда при x=x₁ функция имеет максимум, если f’’(x₁)<0, и минимум, если f’’(x₁)>0
Условие монотонности:
1) Последовательность (a_n) называется возрастающей (неубывающей), если "n<k, nÎN, kÎN a_n£a_k
2) Последовательность (a_n) называется убывающей (невозрастающей), если "n<k, nÎN, kÎN a_n³a_k

Поиск по сайту: