Свойства бесконечно малых функций

Опираясь на правила вычисления пределов, можно сформулировать свойства бесконечно малых: алгебраическая сумма и произведение конечного числа бесконечно малых функций при x → x ₀, а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при x → x ₀:

1.
2.
3.
4.

Все сказанное о бесконечно малых функциях при x → x ₀ справедливо и для бесконечно малых функций при x → ∞, x → + ∞, x → – ∞, x → x ₀ – 0, x → x ₀ + 0.

Сравнение бесконечно малых функций. Пусть a(x) и b(x) - две функции, бесконечно малые в точке x=a. Если

то говорят, что a(x) более высокого порядка малости, чем b(x)и обозначают a(x) =o(b(x)). Если же то b(x) более высокого порядка малости, чем a(x); обозначают b(x) =o(a(x)). Бесконечно малые функции a(x) и b(x) называются бесконечно малыми одного порядка малости, если 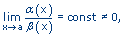обозначают a(x) =const b(x). И, наконец, если

не существует, то бесконечно малые функции a(x) и b(x) несравнимы.

30. Вычисление предела

31. Вычисление предела .

Пусть X>0, угол измеренный в rad. AB=sinx, È AC=x, DC=tgx, очевидно, что AB<AC<ÈAC<DC, sinx<x<tgx, поделим обе части неравенства на sinx: , (1), , , , , , 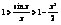т.к. при , , то

, Þ , таким образом, sinx и х являются эквивалентны бесконечно малым величинам, из доказанного предела следует, что

А при x, стремящемся к 0 такой предел (замечательный) =1

32. Непрерывность функции в точке и на интервале. Точка разрыва функции. Односторонние пределы. Примеры.

Пусть ф-я y=f(x), определена на некотором интервале (a;b), пусть , тогда ф-я y=f(x) называется непрерывной на интервале (a;b).

Если ф-я y=f(x) является непрерывной в каждой точке интервала (a;b), то она непрерывна на интервале (a;b) из свойств lim Þ что если ф-я y=f(x) и y=g(x), являются непрерывными в точке, и на интервале (a;b), то их сумма, произведение, частное и произведение f(x) на константу k, также непрерывны в этой точке.

Точки разрыва и их классификация. Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом. Если односторонний предел (см. выше) , то функция называется непрерывной справа рис1. Если односторонний предел (см. выше) , то функция называется непрерывной слева. Рис2

рис2

Рис1

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже. Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Поиск по сайту: