Односторонние пределы. Число А называется левым пределом функции f (x) в точке х0, если для любого как угодно малого положительного числа ε можно найти зависящее от этого

Число А называется левым пределом функции f (x) в точке х ₀, если для любого как угодно малого положительного числа ε можно найти зависящее от этого ε положительное число δ, что для всех значений аргумента меньших чем х ₀ и отличающихся от него на величину меньшую δ, значения функции отличаются от числа А на величину, меньшую чем ε:

( ε > 0) (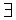 δ = δ (ε) > 0) ( x ₀ - δ < x < x ₀): | f (x) – A | < ε.

Число B называется правым пределом функции f (x) в точке х ₀, если для любого как угодно малого положительного числа ε можно найти зависящее от этого ε положительное число δ, что для всех значений аргумента больших, чем х ₀ и отличающихся от него на величину меньшую чем δ, значения функции отличаются от числа В на величину, меньшую чем ε:

( ε > 0) (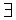 δ = δ (ε) > 0) ( x ₀< x < x ₀+ δ): | f (x) – В | < ε

Левый и правый пределы функции в данной точке условно записывают как

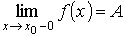и

Теорема. Функция f (x) имеет в точке х ₀ конечный предел тогда и только тогда, когда в этой точке существуют конечные правый и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам.
Доказательство. Пусть

Тогда, согласно определению предела функции слева и справа,

( ε > 0) (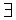 δ₁ = δ₁ (ε) > 0) ( x ₀– δ₁ < x < x ₀): | f (x) – A | < ε.

( ε > 0) (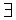 δ₂ = δ₂ (ε) > 0) ( x ₀< x < x ₀+ δ₂): | f (x) – A |<ε

Возьмем δ = min{δ₁,δ₂}. Тогда для всех х, удовлетворяющих неравенствам 0 < | х - х ₀ | < δ, будет выполняться неравенство | f (x) - A | < ε. Что и означает

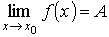
Обратно, пусть

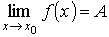
Тогда, по определению предела функции в точке, для любого как угодно малого положительного числа ε > 0 существует зависящее от этого ε число δ > 0 такое, что для всех х, удовлетворяющих неравенству 0 < | х - х ₀| < δ, выполняется неравенство | f (х) – А | < ε. Тем самым, как для х ₀– δ < х < х ₀, так и для х ₀ < x < х ₀ + δ, справедливо неравенство | f (х) – А | < ε. А это,согласно определению односторонних пределов, означает, что

- докажем непрерывность этой ф-ии в некотррой точке х₀:

,

,

, , ,

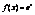
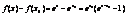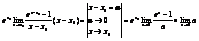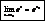
34. Задачи приводящие к понятию производной. Производная ф-ии в точке. Геометрический смысл производной. Уравнение касательной и нормали к графику ф-ий.
Пусть на отр. [a;b] определена ф-ия y=f(x), х₀Î(a;b), рассмотрим 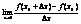(1)
Пусть существует конечное значение lim (1), - это число называют производной ф-ии y=f(x), х=х₀.Обозначается (f’(x), , )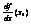
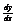При изменении т. х₀ будет манятся значение предела, таким образом можно рассмотреть ф-ию ,

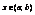
, поэтому , .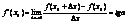
Уравнение касательной:

35. Определение дифференцируемой функции. Дифференциал. Примеры.

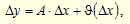
Дифференциал. Пусть на отрезке (a; b) определена функция y = f(x), которая имеет в точке Xo, Xo Î (a; b), тогда принадлежит функции Δf(Xo) = f(Xo + ΔX) – f(Xo) = f ’(Xo)ΔX + 0(ΔX) – 1). Из 1) следует, что принадлежит функции можно представить в виде суммы двух слагаемых. Первые из них являются линейные функции, относят ΔX, а второе является величиной ¥ < более высокого порядка, чем DX. Рассмотрим схему о возможности предоставления приделу произвольной функции. y = f(x) в виде суммы двух слагаемых. Одно из которых является линейным – относительно превращения независимой переменной, а другая является ¥ < более высокого порядка, т. е. f(Xo + DX) – f(Xo) = A + DX + 0(DX) - 2). Первое слагаемое A´ DX – называется главной линейной частью превращения. Определение: Главная линейная часть превращения называется дифференциалом и обозначается следующим образом dy, df(Xo). Разделим левую и правую часть

Пример. Доказать, что функция |x| не дифференцируема в точке x = 0.

Решение. Найдем приращение функции в точке x = 0:

D y = | D x|

Поэтому

lim_{D x ® -0}D y/ D x = -1, lim_{D x ® +0}D y/ D x = 1,

следовательно, функция |x| в точке x = 0 не дифференцируема.

36. Геометрический смысл дифференциала. Пусть задана функция g = f(x), проведем через точку с координатами (Xo; f(Xo)) касательную. Уравнение касательной имеет вид 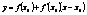. Подставим вместо x значение Xo + DX, тогда получим . Дифференциал df(Xo) равен превращению ординаты касательной, при изменении x от Xo до DX + Xo.

Поиск по сайту: