АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вопрос: Предел функции в точке. Геометрический смысл. Односторонние пределы

Читайте также:
  1. A) эффективное распределение ресурсов
  2. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  3. Access. Базы данных. Определение ключей и составление запросов.
  4. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  5. I. Определите тип придаточного предложения.
  6. I. Определите, какое из этих высказываний несет психологическую информацию.
  7. I. Открытые способы определения поставщика.
  8. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  9. II. Основные задачи и функции
  10. II. Прочтите слова и определите части речи( глаголы, существительные,
  11. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  12. II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ

1.1. Предел функции. Геометрический смысл.

 

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

 

Выясним, в чём заключается геометрический смысл предела функции в точке. Построим график функции 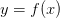и отметим на нём точки и .

 

 

 

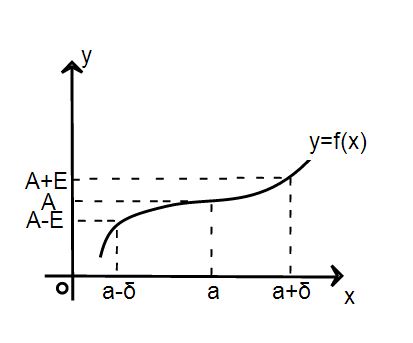
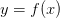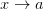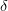Предел функции в точке существует и равен , если для любой -окрестности точки можно указать такую -окрестность точки , что для любого из этой 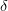-окрестности значение 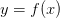будет находится в -окрестности точки .

Отметим, что по определению предела функции в точке для существования предела при 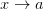не важно, какое значение принимает функция в самой точке . Можно привести примеры, когда функция не определена при или принимает значение, отличное от . Тем не менее, предел может быть равен .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)